Второй этап минимизации
Составление отмеченной таблицы переходов. Составим теперь отмеченную таблицу переходов автомата. Определим вначале внутренние состояния, в которые переходит автомат из состояния 0 при подаче на его вход сигнала x 1. Для этого найдем все предосновные места, содержащие индекс 0, справа от которых записана буква x 1. Таких мест в выражении три. Все основные места, расположенные за этой буквой x 1, отмечены индексом 2. Следовательно, автомат из состояния 0 под действием сигнала x 1 переходит в состояние 2. Аналогично сигнал x 2 переводит автомат из состояния 0 в состояние 1, так как за предосновным местом, содержащим индекс 0, после буквы x 2 расположено основное место с индексом 1. Таким же образом определяются переходы автомата их других внутренних состояний. Сигнал y 1 выдается после поступления подряд трех букв x 1, то есть в состоянии 6, а сигнал y 2 – после x 2, следующей за серией из трех и более букв, то есть в состоянии 8. В остальных случаях выдается пустая буква е. Отсюда получаем следующую отмеченную таблицу переходов.
| yg | e | e | e | e | e | e | y1 | e | y2 |
| xj\ai | |||||||||
| x1 | |||||||||
| x2 |
Из построенной таблицы видно, что из состояний 0, 1, 3 и 5 автомат сигналами x 1 и x 2 переводится в одинаковые состояния (2 и 1). Кроме того, все перечисленные состояния отмечены одинаковыми выходными сигналами. Поэтому состояния 0, 1, 3 и 5 можно объединить в одно состояние, обозначив его как a 0. Введем также обозначения: 2 – a 1; 4 – a 2; 6 – a 3; 7 – a 4; 8 – a 5. Тогда получим упрощенную таблицу переходов автомата. В этой таблице из состояний a 3 и a 4 под действием входных сигналов х 1 и х 2 автомат переходит в одинаковые состояния a 4 и a 5. Но объединять эти состояния нельзя, так как они отмечены разными выходными сигналами. По этой же причине нельзя объединять состояния a 0 и а 5. Объединение состояний и составляет второй этап минимизации, причем объединяются только такие состояния, которые отмечены одинаковыми выходными сигналами, и из которых под действием одинаковых входных сигналов происходит переход в одинаковые состояния. Очевидно, у таких состояний должны совпадать столбцы таблицы переходов.
| yg | e | e | e | y1 | e | y2 |
| xj\ai | a0 | a1 | a2 | a3 | a4 | a5 |
| x1 | a1 | a2 | a3 | a4 | a4 | a1 |
| x2 | a0 | a0 | a0 | a5 | a5 | a0 |
Рассмотрим еще один пример абстрактного синтеза автомата. Найдем таблицу переходов автомата сравнения чисел, условия работы которого заданы регулярными выражениями:
Регулярные выражения
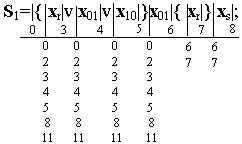
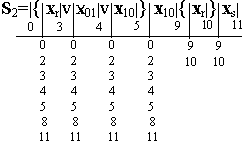
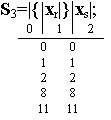
Регулярные выражения событий S 1 и S 2 содержат одинаковые сомножители в итерационных скобках, перед которыми расположено место с индексом 0. Поэтому в обоих выражениях основные места внутри итерационных скобок отмечены одинаковыми индексами (3, 4 и 5). Индекс конечного места каждого выражения распространяется на начальные места всех регулярных выражений, так как в автоматах многократного действия за словом любого события, например S 1, может быть подано слово любого другого события, то есть S 1 v S 2 v S 3. В размеченных выражениях можно объединить места с индексами 4, 6 и 5, 9:
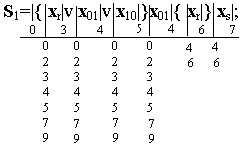
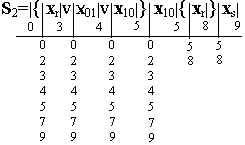
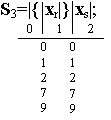
По размеченному выражению составим отмеченную таблицу переходов.
| yg | е | е | y3 | е | е | е | е | y1 | е | y2 | е | е | е | е |
| xj\ai | 1v3 | 3v6 | 3v8 | * | ||||||||||
| xr | 1v3 | 1v3 | 3v6 | 3v8 | 1v3 | 1v3 | 1v3 | 3v6 | 3v8 | * | ||||
| x01 | * | * | * | * | ||||||||||
| x10 | * | * | * | * | ||||||||||
| xs | * | * |
При составлении таблицы следует учитывать, что для разных регулярных выражений автомат под действием одних и тех же входных сигналов переходит в разные состояния. Эти внутренние состояния будем отмечать множеством индексов основных мест. Например. В событии S 3 переход из состояния 0 в состояние 1 происходит под действием сигнала x r а в S 1 под действием этого же сигнала из состояния 0 автомат переходит в состояние 3. Поэтому, внутреннее состояние, в которое автомат переходит под действием xr из состояния 0, будем обозначать множеством из двух индексов 1 v 3. Аналогично получается переход из состояний 2, 7 и 9 под действием x r, а также переход из состояния 4 и 5 в состояния 3 v 6 и 3 v 8 соответственно под действием x r. При заполнении таблицы получается свободные клетки там, где переходы в автомате не определенны. Такие клетки будем отмечать звездочкой *, которую следует рассматривать как индекс некоторого внутреннего состояния. Таблица переходов составляется не только для состояний, отмеченных индексами основных мест регулярного выражения, но и для состояний, отмеченных множеством индексов. Для заполнения колонок для таких состояний достаточно образовать дизъюнкцию таких индексов, которые расположены в колонках, отмеченных индексами, входящими в множества. Например. Для заполнения колонки 1 v 3 образуем дизъюнкцию индексов расположенных в колонках 1 и 3. Поскольку состояния 1, 3, 6 и 8 отмечены пустой буквой e, то и состояния 1 v 3, 3 v 6, 3 v 8 также отмечаются буквой е.
После построения таблицы проведем второй этап минимизации числа внутренних состояний автомата. Можно объединить состояния, отмеченные индексами: 0 и 1v3, 4 и 3v6, 5 и 3v8. При этом состояния отмеченные звездочкой обозначим через 10, а состояния 1v3 – 0, 3v6 – 4, 3v8 – 5.
| yg | e | e | y3 | e | e | e | e | y1 | e | y2 | e |
| xj\ai | |||||||||||
| xr | |||||||||||
| X01 | |||||||||||
| X10 | |||||||||||
| xs |
По построенной таблице проведем третий этап минимизации, исключив такие состояния, в которые автомат из нулевого состояния никогда перейти не может. В нашем случае такими состояниями являются 1, 3, 6, 8 и 10.
Обозначив оставшиеся состояния 0 – b 0, 2 – b 1, 4 – b 2, 5 – b 3, 7 – b 4, 9 – b 5, получим окончательную таблицу переходов заданного автомата.
| yg | e | y3 | e | e | y1 | y2 |
| xj\ai | b0 | b1 | b2 | b3 | b4 | b5 |
| xr | b0 | b0 | b2 | b3 | b0 | b0 |
| x01 | b2 | b2 | b2 | b2 | b2 | b2 |
| x10 | b3 | b3 | b3 | b3 | b3 | b3 |
| xs | b1 | b1 | b4 | b5 | b1 | b1 |
 2014-02-09
2014-02-09 613
613








