Момент инерцииматериальной точки относительно неподвижной оси вращения равен произведению её массы на квадрат расстояния до рассматриваемой оси вращения
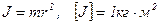 .
.
Момент инерции тела равен сумме моментов инерции всех его точек:
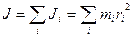 .
.
1. Момент инерции обруча (толщиной стенок пренебрегаем) или полого цилиндра:

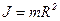 .
.
2. Момент инерции диска или сплошного цилиндра радиуса R:


,
3. Момент инерции шара

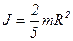 .
.
4. Момент инерции стержня

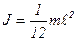 .
.
Теорема Штейнера: момент инерции тела относительно произвольной оси равен моменту инерции J0 относительно оси, параллельной данной и проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями.

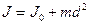 ,
,
где d расстояние от центра масс О до оси вращения (рис.).
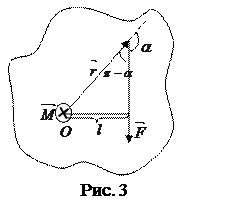 Моментом силы относительно точки О называется векторная величина, равная векторному произведению радиус-вектора
Моментом силы относительно точки О называется векторная величина, равная векторному произведению радиус-вектора 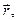 проведенного из точки О в точку приложения силы, на вектор силы:
проведенного из точки О в точку приложения силы, на вектор силы: 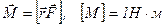 .
.
Модуль момента силы численно равен произведению силы на плечо:
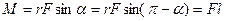 ,
,
где 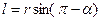 - плечо силы относительно точки О, a - угол между направлениями
- плечо силы относительно точки О, a - угол между направлениями 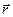 и
и 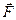 ,
, 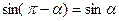 .
.
Плечо - кратчайшее расстояние от центра вращения до линии действия силы.
Моментом силы относительно неподвижной оси Z называется проекция вектора 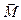 на эту ось (проходящую через точку О):
на эту ось (проходящую через точку О):
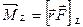 .
.
 2014-02-09
2014-02-09 651
651








