2014-02-09
600
Математические модели функционирования информационно-измерительных и управляющих систем
Лекция 5.
2.1.1. Определение математической модели
В широком смысле на практике под математической структурой системы следует понимать способ описания и форму представления её элементов, свойств и связей. При этом под математической структурой в узком смысле следует понимать только строение системы как совокупность конечного числа элементов, вид и направление согласующих связей между ними, и их преобразующие свойства. Тогда математическая структура системы в широком смысле представляет собой совокупность отношений и отображений, задающих упорядоченные связи и элементы в системе. На практике для построения математической модели системы вполне достаточно определения математической структуры первого порядка, называемой просто математической структурой, под которой будем понимать выражение следующего вида:
 
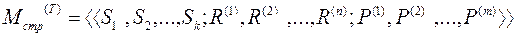
| (2.1.1) |
где приняты следующие обозначения: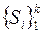 
- множество математических элементов различных по функциональным действиям, назначениям и наименованиям; 
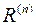- n -местным (n -мерным) отношением на непустом множестве 
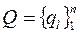(в общем случае 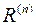представляет собой подмножество декартова произведения n -ой степени); 
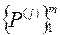– множество отображений множества 
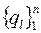во множество
.
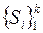Одним из наиболее ярких применений понятия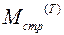 
при теоретическом анализе процесса преобразования информации является модельное описание системы. Построенная 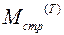системы может быть в узком смысле принята за математическую модель её, если элементы и связи между ними для 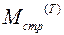могут отображать реальные свойства системы. Таким образом, чтобы избежать не однозначного трактования результатов математического моделирования необходимо в 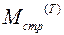установление взаимно однозначного соответствия (изоморфизма) между её компонентами.
Введение понятия 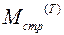дает возможность перейти к понятию математической модели системы. Полнота математической модели определяет степень однозначности модельного представления системы. Математические модели можно классифицировать [13]:
- Непрерывные линейные модели, описываемые системой линейных дифференциальных уравнений вида:
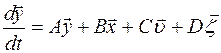
| (2.1.2) |
где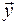 
- n - мерный вектор выходного сигнала; 
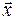- r - мерный вектор входного сигнала; 
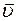- m - мерный вектор управления; 
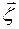- k - мерный вектор возмущающего воздействия; A – (n´n) - мерная постоянная матрица; B - (n´r) - мерная постоянная матрица; C - (n´m) - мерная постоянная матрица; D - (n´k) - мерная постоянная матрица.
- Непрерывные нелинейные модели, описываемые системой нелинейных дифференциальных уравнений вида
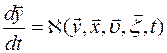
| (2.1.3) |
- Дискретные линейные модели, описываемые для постоянного временного интервала разностными уравнениями вида:
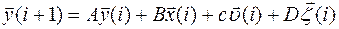
| (2.1.4) |
где i = 0,1,2,…, N -1 – номер временного интервала.
- Дискретные нелинейные модели, описываемые разностными уравнениями вида:
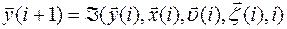
| (2.1.5) |
- Стохастические модели.
- Нечёткие модели.
- Логико-вероятностные модели с неизменяющейся вероятностью событий.
- Логико-вероятностные модели с изменяющейся во времени вероятностью событий.
- Логико-вероятностные модели с интервальным заданием вероятностей событий.
- Логико-вероятностные модели с интервальным заданием вероятностей, изменяющимися во времени.
- Логико-вероятностные модели со случайными вероятностями событий и изменяющимися во времени их плотностями распределения.
- Логико-лингвистические модели с неизменяющимися во времени функциями принадлежности.
- Логико-лингвистические модели с изменяющимися во времени функциями принадлежности.
- Логико-лингвистические модели с неформализуемыми атрибутами лингвистического типа.
В дальнейшем применительно к рассматриваемому в книге классу систем, а именно ИУСО мы будем рассматривать только первые три модели применительно к имитационному моделированию, а именно для рассматриваемых в книге вопросов связанных с имитационным моделированием технических систем обобщённая математическая модель которой в соответствии с соотношением 2.1.5 представим в следующем виде:
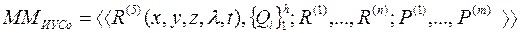
| 2.1.6 |
где приняты следующие обозначения: x, y, z – пространственные координаты; l - рабочий спектральный диапазон излучения; t – время;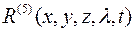 
- пространственно-временная и спектральная характеристика объекта; 
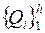, - основные множества математических элементов разной природы, различающихся условно приписываемыми им названиями.
