Структурная схемаинформационно-измерительной и управляющей системы
Как отмечалось выше, сущность методологии математического моделирования состоит в замене исходной системы её «образом» - математической структурой, выражающей с помощью математической символики её математическую модель, отражающая свойства этой системы.
Как отмечалось в 1.2 для представления ИУС математической моделью на любом из уровней необходимо произвести дискретизацию системы, что в соответствии с обобщенной её структурой (см.рис.1.2.2) и представлено на рис. 2.2.1, где приведена структурная схема ИУС, работающей в оптическом диапазоне длин волн относительно входной информации (далее по тексту - ИУСО).
На рис. 2.2.1 приняты следующие обозначения: НО t0 – наблюдаемый объект в момент времени t; НО tР –прогнозируемое положение НО на момент расчетного времени tР; НО tВ – реальное положение НО на момент времени «встреча»; СПЦУ – система ввода предварительной информации о положении НО; ПОС – приёмная оптическая система ИУС(аппаратура оптического визирования и измерения текущих пространнственно-временных пара-метров НО); ПУ – пульт управления и преобразования вида сигналов; УС – устройство связи между объектом управления и ПОС (обеспечивает информацией о взаимном текущем положении между направлением на НО и линией визирования); ИС – исполнительная система управления линией визирования; ЦВМ – цифровая вычислительная машина; S – вектор пути НО за время отведённое для решения поставленной перед ИУСО; h – вектор «промаха»; 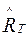 - оценка вектора положения НО t0;
- оценка вектора положения НО t0; 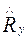 - вектор прогнозируемого положения НО tР; Y ПОС – ошибки визирования и измерения в ПОС; Y КЗвена – ошибки кинематического звена.
- вектор прогнозируемого положения НО tР; Y ПОС – ошибки визирования и измерения в ПОС; Y КЗвена – ошибки кинематического звена.

Функционирование ИУСО заключается в выполнении следующих действий:
1. На вход исполнительного устройства от СПЦУ поступает информация о возможном местонахождении НО.
2. Исполнительное устройство ориентирует линию визирования ПОС в нужном направлении.
3. «Оператор» (человек или автомат) осуществляет поиск, обнаружение и распознавание НО в пределах поля зрения ИУСО, в соответствии с его информационными признаками.
4. «Оператор» в соответствии с выбранным заранее методом совмещения линии визирования с направлением на НО (метод наведения) осуществляет передачу информацию о пространственно-временных параметрах НО через пульт управления на формирователь управляющих сигналов.
5. Формирователь управления, выполняющий и функцию экстраполятора, в соответствии с расчетными значениями из ЦВМ и параметров наведения с ПУ формирует управляющие сигналы для КСУ.
6. КСУ в соответствии с выбранной системой координат и методами наведения и парирования внешних механических возмущений, осуществляет необходимое позиционирование объекта управления.
Соответствующая (2.2.1) математическая модель ИУСО на макроуровне по принципу «вход-выход» может быть представлена в виде дифференциальных уравнений – нормальная форма представления
 | (2.2.1) |
где 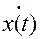 - вектор состояния системы по входу x(t); u - вектор управлений;y - вектор выхода; z - вектор измерений; Ri – множество состояний (i = n, m, l, q, k); A, B, C, D и G - матрицы параметров, определяющих функционирование системы.
- вектор состояния системы по входу x(t); u - вектор управлений;y - вектор выхода; z - вектор измерений; Ri – множество состояний (i = n, m, l, q, k); A, B, C, D и G - матрицы параметров, определяющих функционирование системы.
В матричном виде эта же модель, но уже учитывающая структуру ИУСО, может быть представлена в следующем виде, где МО и M/O - матрица лучей, входящих и выходящих из оптической системы;  - матрица, представляющая собой оператор действия ПОС;
- матрица, представляющая собой оператор действия ПОС;  - матрица, учитывающая движение НО;
- матрица, учитывающая движение НО;  - вектор перемещения линии визирования ИУСО в пространстве;
- вектор перемещения линии визирования ИУСО в пространстве; 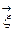 - вектор внешних помех;
- вектор внешних помех; 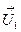 -вектор управления линией визирования; М2 -матрица постоянных коэффициентов.
-вектор управления линией визирования; М2 -матрица постоянных коэффициентов.
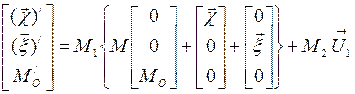 | (2.2.2) |
Хотя и 2.2.1, и 2.2.2 являются «образом» ИУСО, но 2.2.2 отражает помимо происходящих процессов и структуру системы, а 2.2.1 только процессы.
Следует отметить, что вектор «промаха» определяется как:
1. Вектор расхождения моделей  , между моделью вектора свойств системы
, между моделью вектора свойств системы 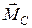 и моделью реального описания этих свойств
и моделью реального описания этих свойств 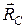 . При этом надо учитывать: модель текущего положения НО t0 (вектор - Rt);модель прогнозируемого положения НО tР (вектор - R У - своего родамодель вектора «встречи».
. При этом надо учитывать: модель текущего положения НО t0 (вектор - Rt);модель прогнозируемого положения НО tР (вектор - R У - своего родамодель вектора «встречи».
2. Норма вектора «промаха» определяется
- Методические – погрешности, происходящие от несовершенства метода измерений, допущений, положенных в основу теории выбранного метода измерений (приближенная формула; округление измерений и управления).
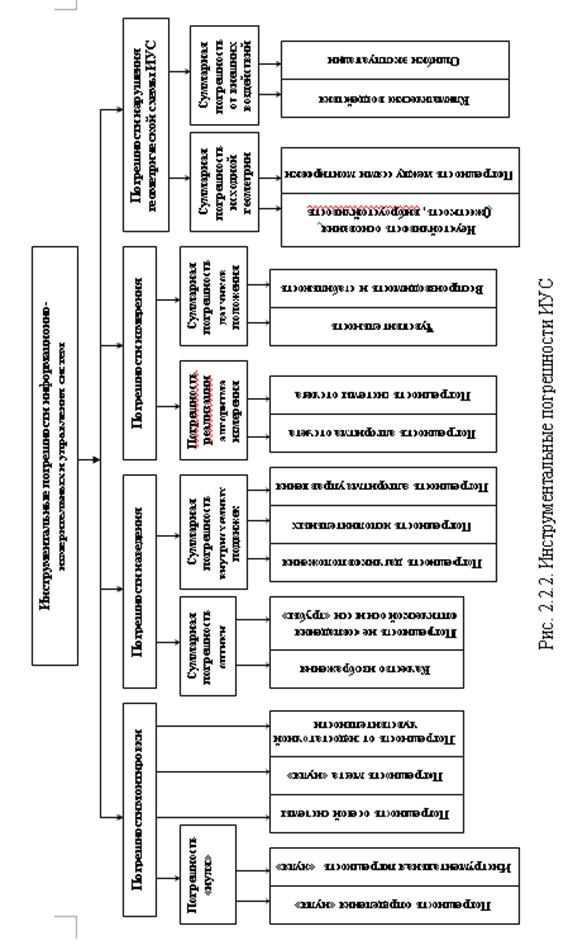
- Инструментальные – погрешность монтировки (мера не совпадения ориентировки осей телескопа с выбранной системой координат); правильность определения направления на наблюдаемый объект; ошибка отсчета; ошибка сопровождения наблюдаемого объекта - динамическая погрешность.
- Субъективные – погрешность работы «оператора».
- Внешние – несанкционированные воздействия на ИУС.
В частности на рис.2.2.2 представлены возможные инструментальные погрешности ИУС
Внешние воздействия на ИУСО, характеризуются случайной многомерной функцией. Обычно характер возмущающего воздействия нельзя считать детерминированной функцией времени. Однако эти функции могут быть проанализированы с применением математического аппарата теории вероятности и случайных функций, при этом математическое ожидание можно принять равным нулю[50,52,70]. Однако каждому типу возмущений соответствуют свои типы компенсирующих систем, позволяющие осуществлять частичную или полную их компенсацию. В этой связи не может быть принципиально создана система, которая устраняла бы полностью последствия внешнего воздействия на ИУСО, тем самым всегда остаются остаточные последствия от воздействия внешних возмущений.
Действия внешних факторов на ИУСО, влияющих на качество её функционирования, могут быть вызваны следующими видами возмущений и помех:
- механическими - угловые перемещения, различные по амплитуде и частоте (качка); линейные перемещения, различные по амплитуде и частоте;
- кратковременное силовое воздействие (удар);
- электромагнитными;
- тепловыми;
- химическими (включая воздействие и воды);
- радиационными (радиация, облучение);
- атмосферными.
Математическая модель ИУСО на более высоком уровне иерархии может быть представлена в виде совокупности математических моделей её подсистем, основные из которых будут представлены ниже.
Ниже представлены математические модели подсистем ИУСО, которые могут быть положены в основу имитационного моделирования.
===============
 2014-02-09
2014-02-09 1124
1124
