Лекция 6. Математическая модель технической системы

Математическая модель технической системы

Проблемы математической теории

Анализ задачи начинается с проблемы описания используемых в математической модели основных множеств S_k, элементы которых оказывают влияние на поведение системы. По существу, это проблема описания множеств входных S ={ s } и выходных å ={ s } сигналов, определенных например для ИУС_О в областях D_s(x, y, z, l, t) и D_å(x, y, z, l, t), задаваемых некоторой математической структурой áá R_D; d ññ в пятимерном векторном пространстве R ⁵(x, y, z, l, t). В рамках концептуальной модели описываются конечные множества преобразующих элементов (звеньев) В= { b }, а также внутренних G= { g } и внешних Q= { q } параметров. Далее ставится задача определения взаимосвязей между входными и выходными сигналами с учетом связей между элементами и параметрами. Иначе говоря, возникает проблема идентификации, то есть задача построения по результатам наблюдения некоторого запаса отношений R _l и отображений P_n, которые описывают систему. Например, выделение подмножеств конкретных сигналов на входе и выходе ИУС_О соответствует построению унарных отношений, т.е. “быть входным или выходным сигналом” на множествах S и å. Внутренние и внешние параметры задаются в виде упорядоченных векторов g =(g₁,...,g_m) и q =(q₁,...,q_n) с помощью m-арного R^m(g₁,...,g_m) и n-арного Rⁿ(q₁,...,q_m) отношений. Отношения определяются как подмножество R^mÌG´...´G декартова m-ой степени произведения множеств G и подмножество RⁿÌQ´...´Q декартова n-ой степени произведения множеств Q. Введение различных отношений на множестве В= { b } звеньев ИУС_О указывает, какие звенья и в каком порядке связаны с друг другом. Что касается запаса отображений, то их количество и вид зависят от реальной системы.

Для динамической системы решением проблемы идентификации является также множество U={u} фазовых переменных или переменных состояния, являющееся фундаментальным понятием теории систем. Фазовые переменные возникают из-за того, что при формальном анализе характера зависимости выхода динамической системы от входа обнаруживается, что непосредственной связи между ними нет. Предысторию входов (причин) до момента времени t и выход в этот момент связывают фазовые переменные. Они характеризуют физическое или информационное состояние системы, а их изменения во времени выражают переходные процессы в динамической системе. Следует отметить, что, так как переходные процессы в оптических преобразующих элементах протекают со скоростью света, то эти преобразующие элементы, могут рассматриваться как стационарные подсистемы, динамика поведения которых не имеет практического значения. Поэтому, если не касаться проблем адаптивной оптики, то можно принять допущение об отсутствии фазовых искажений в оптическом тракте ИУС_О.

С проблемой идентификации прежде всего связана другая основная проблема - проблема представления системы, где изучаются возможные описания закономерностей поведения преобразующих элементов или всей ИУС_О.

В рамках анализа системы также представляет интерес задача прогноза выхода s(x’,y’,t) по наблюдаемому входу s(x,y,t), называемая проблемой наблюдаемости, возникающая из необходимости прогнозирования будущего поведения системы.

Следующая проблема теории систем связана с исследованием разрешимости задач формирования специального поведения, например, адаптивных ИУС_О и вызывается необходимостью удовлетворения определенных требований, накладываемых процессом преобразования сигналов. Эти требования — цель, которая ставиться перед системой.

Для учета влияния входных сигналов на поведение системы выделяют два подмножества. Элементы одного из них не зависят от наблюдателя и называются возмущениями, а элементы другого — управлениями. Систему, цель и исходные данные, на основании которых должна решаться задача нахождения управлений, обеспечивающих достижение цели, называют проблемой управления.

Чтобы сравнивать между собой по эффективности функционирования разные ИУС_О, необходимо иметь какой-то количественный критерий, так называемый показатель эффективности, и функциональный критерий целевая функция. Целевая функция выбирается так, чтобы она отражала целевую направленность ИУС_О. Лучшей будет считаться та система, у которой «разница» между реализованной целевой функцией и требуемой минимальна.

Цель математического моделирования ИУС_О — заменить реальную систему её модельным описанием, доступной для теоретического изучения. Модельное описание ИУС_О в определенном смысле проще самой системы, так как оно отражает не все, а лишь наиболее важные особенности самой системы и поэтому удобнее для изучения.

Несмотря на разнообразие систем, целей и методов их исследования, в конечном счете, в результате математического моделирования ИУС_О решаются три основные задачи:

· модельное описание процесса прохождения информации в системе в определенных условиях при наличии внешних возмущающих факторов;

· выявление разнообразия структуры ИУС_О, механизмов, управляющих их поведением, и способов целенаправленного воздействия на систему;

· экстраполяционная задача построения математической модели ИУС_О как объекта проектирования для выполнения базовых проектных процедур анализа, синтеза и структурно-параметрической оптимизации.

Математическая модель системы в общем случае есть совокупность математических объектов и отношений между ними, адекватно отображающие её свойства. При этом полная модель системы есть система уравнений [69,72 ] (Курейчик-?)

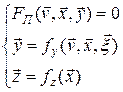(2.1.4)

где 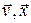- векторы внутренних и входных переменных; 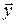- вектор выходных переменных; 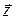- вектор измерений или оценок; 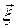- вектор внешних возмущений. Размерность 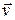и порядок системы (2.1.4) определяется количеством функционально динамических элементов в технической системе. В этой связи требуется упрощения, если порядок системы становится чрезмерно большим, тем самым перейти на другой более высокий уровень, например, представить модель системы без учета внутренних переменных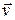, т.е. представление ТС макромоделью (2.1.5).

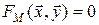(2.1.5)

При этом 2.1.4 и 2.1.5 относятся друг к другу как полная модель системы и макромодель на n -м уровне иерархии. На более высоком (n -1)-м уровне системы представляется подсистемой для (n -1)-го уровня, т.е. учитываются более сложные связи, которые на n -м уровне не рассматривались. Тем самым соотношение 2.1.4 является идеализированным представлением ТС, т.к. не учитывает внутренние свойства её подсистем.

Возможны следующие формы представления моделей ИУС_О, а именно:

1. Инвариантная форма - представление ТС математическим описанием инвариантным к методу решения уравнений.

1. Алгоритмическая форма (алгоритмические модели) – запись соотношений модели и выбранного метода решения в форме алгоритма.

1. Аналитическая форма (аналитические модели) – запись соотношений по форме «вход-выход» в аналитическом виде.

1. Схемная (графическая) форма – представление модели на графическом языке, например в виде графов.

Основные требования, предъявляемые к математическим моделям технических систем.

Адекватность модельного представления свойств системы (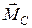) обеспечивается минимизацией вектора расхождений 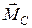относительно реального и действительного описания свойств системы - 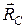, вектор расхождения - 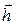в общем случае представим в следующем виде:

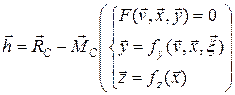(2.1.6)

Универсальность модели определяется числом учитываемых как внешних, так и внутренних параметров.

Экономичность модели определяется стоимостными затратами.

При описании функциональных моделей ТС в одной из форм представления применяются теоретические и экспериментальные методы получения, основанные на физических закономерностях и данных о внешних проявлениях. Хотя многие операции моделирования носят эвристический характер, тем не менее, ряд положений и приемов носят общий характер, а именно относительно этапов моделирования:

1. Определение свойств системы, отражаемых в модели.

1. Сбор априорной информации о свойствах системы.

1. Определение параметров .

1. Выбор краевых условий и ограничений для .

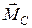1. Выбор формы представления .

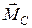1. Представление 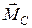в одной из форм (инвариантная, аналитическая, алгоритмическая, схемная).

1. Оценка области адекватности .

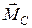1. Определение точности полученной .

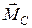1. Преобразовать модель в компьютерно-ориентированный вид.

1. Разработка языка взаимодействия человека с ЭВМ.

1. Разработка формы представления результатов моделирования.

Математические модели ИУС на макроуровне могут быть представлены в виде компонентных и топологических уравнений. Математические модели подсистем системы представимы в виде компонентных уравнений. Математические модели, отображающие связи между подсистемами представимы в виде топологических уравнений. Одним из условий создания моделей на макроуровне является структурирование ТС на физически однородные подсистемы.

В физически однородных подсистемах систем различают три типа простых элементов – это элементы емкостного, индукционного и резистивного типа и соответствующие их модели имеют вид [Курейчик?]:

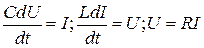(2.1.7)

Физический смысл C,U,I, L и R поясняется в таблице 2.1.1.

Форма представления математических моделей на макроуровне, определяется используемыми языковыми средствами. Однако следует отметить, что наряду с традиционным математическим языком применяют:

· алгоритмические языки;

· графические изображения, облегчающие пользователю восприятие модели, в виде эквивалентных схем, графов и шаблонов.

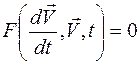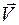В общем случае математическая модель ИУС, функционирующей на основе физических законов, на макроуровне представляет собой систему дифференциальных уравнений , где - вектор базисных координат, t – время. В основном применяются следующие формы представления математической модели ТС на макроуровне:

• нормальная форма ;

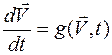• линеаризованная форма ;

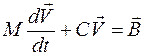• алгебраизованная и линеаризованная форма .

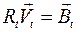Следует отметить, что, как правило, линеаризацию выполняют путем разложения вектора 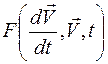в ряд Тейлора с сохранением только линейных членов.

Таблица 2.1.1

Подсистема	Тип фазовой переменной	Параметры простых элементов
потенциал U	поток I	C	L	R
механическая	скорость	сила	масса	Гибкость (обратная величина -жесткость	механическое сопро-тивление
механическая вращательная	угловая скорость	вращательный момент	момент инерции	вращательная гибкость	вращательное сопротивление
электрическая	электрическое напряжение	электрический ток	электрическая ёмкость	электрическая индуктивность	электрическое сопро-тивление
тепловая	температура	тепловой поток	теплоёмкость	-	тепловое сопротивление
гидравлическая (пневматическая)	давление	расход	гидравлическая (пневматическая) ёмкость	Гидравлическая (пне- вматическая)инду-ктивность	Гидравли ческое (пневмати ческое)соп-ротивление
оптическая	оптическая сила	световой поток	длина хода луча	увеличение	поглощение

Математические модели подсистем ИУС на микроуровне отражают физические процессы, протекающие непрерывно во времени. Независимыми переменными физического процесса являются пространственно-временные координаты, а зависимыми - фазовые переменные. Взаимосвязи переменных выражаются с помощью уравнений математической физики, которые и составляют основу математических моделей подсистем ИУС на микроуровне.

Процессы, протекающие в каждом типе подсистем (см. табл.2.1.1) основаны на определённых уравнениях математической физики. При этом для получения математической модели на микроуровне следует выполнить ряд процедур:

• выбрать краевые условия, представляющие собой значения фазовых переменных и их производных на границе пространственно-временной области;

• дискретизировать систему с целью разделения пространственно-временной областей на конечное число таким образом, чтобы число фазовых переменных также было конечно;

• аппроксимировать дифференциальные и интегральные уравнения алгебраическими уравнениями (алгебраизировать задачу).

Обобщенная форма записи уравнений для большинства моделей ИУС на микроуровне - 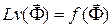, где L - дифференциальный оператор; 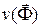- зависимая фазовая переменная; 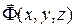- вектор независимых координат; 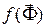- заданная функция. Лаконичная запись нестационарных уравнений имеет следующий вид 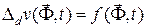, где 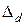- где дифференциальный оператор, включающий дифференцирование по всем независимым переменным. Для полноты представления ТС математической моделью на микроуровне необходимо и уравнения краевых условий, общий вид которых - 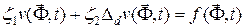, где 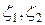- коэффициенты.

Математические модели ИУС на метауровне получают путем дальнейшего абстрагирования от характера физических процессов протекающих в системе с выделением для моделирования уже элементов подсистем. Математические модели на метауровне – это системы дифференциальных и логических уравнений, имитационные модели.

=====================