Решение типовых задач. Пример 1. Имеются следующие данные об объеме товарооборота торговых центров

Пример 1. Имеются следующие данные об объеме товарооборота торговых центров.

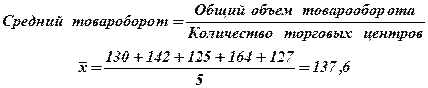
Формула данного вида средней следующая:

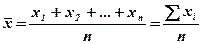
Пример 2. Определите среднюю выработку одного рабочего за рабочую смену по следующим данным (продукция однотипная):

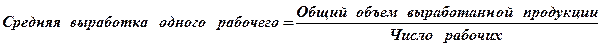
В логической формуле известны значения знаменателя, но не известны значения числителя, поэтому средняя вычисляется по формуле средней арифметической взвешенной.

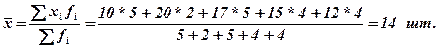
Пример 3. Две автомашины прошли один и тот же путь: одна – со скоростью 70 км/ч, а вторая – 90 км/ч. Тогда средняя скорость составит:

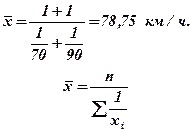
Пример 4. Определите среднюю себестоимость продукции предприятия по следующим данным:

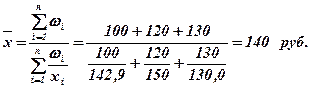
Пример 5. По следующим данным о распределении 100 рабочих цеха по дневной выработке однотипных изделий определите моду и медиану:

Определим моду:

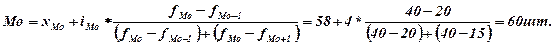
Определим медианный интервал. Им считается тот, до которого сумма накопленных частот меньше половины всей численности ряда, а с прибавлением его численности – больше половины. Подсчитаем накопленные итоги частот: 10, 30, 70, 85, 100. Середина накопленных частот – 100/2=50. Сумма первых двух меньше половины (30<50), а если прибавить 40 – больше половины численности совокупности (70>50). Следовательно, медианным является интервал – 58-62. Определим медиану:

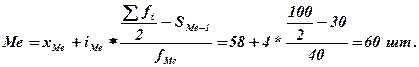
Итак, 50% рабочих вырабатывают в день меньше 60 изделий, а остальные 50% – более 60 шт.