Распределение вероятности в малых выборках в зависимости
Таблица 7.3.
 n n
| ∞ | |||||||||
| t | ||||||||||
| 0,5 | 0,348 | 0,356 | 0,362 | 0,366 | 0,368 | 0,370 | 0,372 | 0,376 | 0,378 | 0,383 |
| 1,0 | 0,608 | 0,626 | 0,636 | 0,644 | 0,650 | 0,654 | 0,656 | 0,666 | 0,670 | 0,683 |
| 1,5 | 0,770 | 0,792 | 0,806 | 0,816 | 0,832 | 0,828 | 0,832 | 0,846 | 0,850 | 0,865 |
| 2,0 | 0,860 | 0,884 | 0,908 | 0,908 | 0,914 | 0,920 | 0,924 | 0,936 | 0,940 | 0,954 |
| 2,5 | 0,933 | 0,946 | 0,955 | 0,959 | 0,963 | 0,966 | 0,968 | 0,975 | 0,978 | 0,988 |
| 3,0 | 0,942 | 0,960 | 0,970 | 0,976 | 0,980 | 0,938 | 0,984 | 0,992 | 0,992 | 0,997 |
Независимо от вида выборки, на заключительном этапе определяются доверительные интервалы, в которых может находиться генеральная средняя (для количественных признаков) или генеральная доля (для качественных признаков). Доверительные интервалы – это область тех значений генеральной средней, выход за пределы которой имеет весьма малую вероятность. Доверительные интервалы определяются по формулам:
· для средней:  ;
;
· для доли: 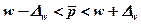 ;
;
· для малой выборки: 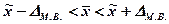
 2014-02-09
2014-02-09 675
675








