Синтез информационных систем с заданным временем ответа

Задача синтеза информационной системы заданной стоимости

Обслуживается поток λ₀. Суммарная стоимость устройств информационной системы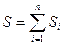

Известны характеристики класса задач, т.е. определены потребные ресурсы для решения каждой задачи.

В качестве модели информационной системы используем разомкнутую сеть, состоящую их n СМО, каждая СМО соответствует одному устройству.

На вход i-го устройства поступает поток: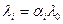

α_i – коэффициент передачи

Средняя длительность обслуживания: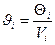

Интенсивность обслуживания: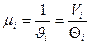

Время ответа для i-ой СМО: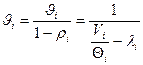

Время ответа для сети: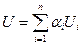

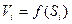
Допущение: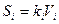

Количество у.е., которое необходимо выделить на создание информационного комплекса:

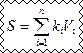
S₁ S₂ … S_n

↓ ↓ ↓

V₁ V₂ … V_n

Лагранжиан: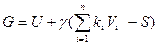

γ – неопределенный множитель Лагранжа

Дифференцируем функцию G по быстродействию:

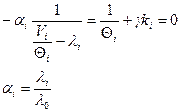
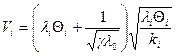
Умножим на k_i и суммируем по i:

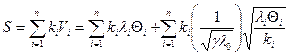
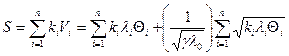
Откуда

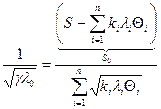
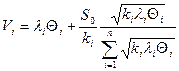
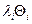-на обеспечение существования стационарного режима в системе

(небесконечная очередь)

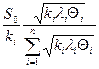Минимизация времени ответа

Построить информационную систему, обеспечивающую обслуживание интенсивности задач λ₀, чтобы U_ОТВ ≤ U*, а стоимость системы была бы минимальной.

Модель – разомкнутая СеМО.

Построим функцию Лагранжа: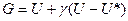

γ – неопределенный множитель Лагранжа

Дифференцируем по V и приравниваем нулю:

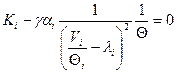
Откуда: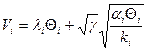

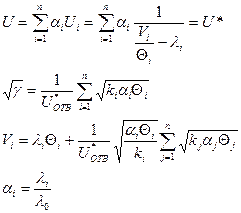
Первое слагаемое обеспечивает стационарный режим. Второе слагаемое обеспечивает минимизацию стоимости и обеспечивает нужное время ответа.

Нами были рассмотрены некоторые простейшие модели массового обслуживания, которые могут быть применены для предварительного анализа ИС и определения их характеристик. Их использование на этапе эскизного проектирования позволяет более осознанно подходить к выбору технических и программных средств для ИС.