С бесконечно высокими стенками

Микрочастица в прямоугольной потенциальной яме

Рис.9.2

Предположим, что частица может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U имеет в этом случае следующий вид (рис. 9.2а): она равна нулю при 0 ≤ х ≤ l и обращается в бесконечность при х <0 и х > l.

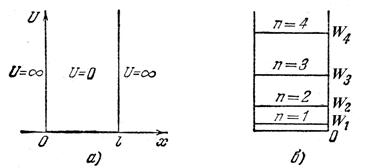
Найдем собственные значения энергии и соответствующие собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме.

Поскольку пси-функция зависит только от координаты х, уравнение Шредингера упрощается следующим образом:

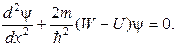(9.3)

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружить частицу, а следовательно, и функция ψза пределами ямы равна нулю. Из условия непрерывности следует, что ψдолжна быть равна нулю и на границы ямы, т. е.

что Ψ(0) = ψ(l) = 0. (9.4)

В области, где ψтождественно не равна нулю уравнение (9.3), имеет вид:

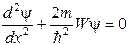. (9.5)

Введя обозначение

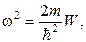(9.6)

придем к уравнению, хорошо известному из теории колебаний:

ψ ^''+ ω ² ψ = 0.

Решение такого уравнения имеет вид:

Ψ (х) = А sin(ωx + α). (9.7)

Из условия Ψ (0) = 0 получаем

Ψ (0) = А sin α = 0,

откуда следует, что α должна быть равна нулю. Далее должно выполняться условие:

Ψ (l) = А sin ωl = 0,

что возможно лишь в случае, если

ωl = ± nπ (n = 1, 2, 3, …). (9.8)

Из уравнений (9.6) и (9.8) найдем собственные значения энергии частицы:

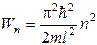(n = 1, 2, 3, …). (9.9)

Спектр энергии оказался дискретным. На рис. 9.2б изображена схема энергетических уровней.

Оценим расстояние между соседними уровнями для различных значений массы частицы m и ширины ямы l. Разность энергии двух соседних уровней равна

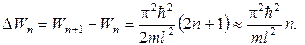
Если взять m порядка массы электрона (9,1∙ 10^{-31 кг), а} l порядка 0,1 м (электрон в сосуде), получим 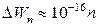эВ. Столь густо расположенные энергетические уровни будут восприниматься как сплошной спектр энергии. Однако совсем иной результат получится для электрона, если область, в которой он движется, будет порядка атомных размеров (~ 10^{-10 м). В этом случае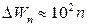} эВ, так что дискретность энергетических уровней будет весьма заметной.

Подставив в (9.7) значение ω, найдем собственные функции задачи:

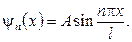
Для нахождения А воспользуемся условием нормировки, которое в данном случае запишется следующим образом:

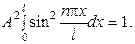
В результате получим, что А = 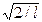. Таким образом, собственные функции имеют вид:

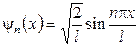(n = 1, 2, 3, …). (9.10)

Графики собственных функций изображены на рис. 9.3 а.

Рис. 9.3

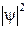На рис.9.3 б приведена плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная . Из графика видно, что, например, в состоянии с n = 2частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.

Лекция 10