Министерство аграрной политики и продовольствия Украины
6.
5.
4.
3.
2.
1.
В аналитической геометрии поверхность рассматривается как геометрическое место точек, её составляющих.
Пусть М – произвольная (текущая) точка этой поверхности. Положение точки М должно подчиняться определенному условию, характеризующему эту поверхность. Так как положение точки М определяется её координатами x, y, z,, то условие, которому должно удовлетворять положение точки М, сводится к условию, которому должны удовлетворять координаты точки М, т.е. сводится к некоторому уравнению.
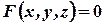 (1)
(1)
Это уравнение называют уравнением данной поверхности, если координаты любой точки поверхности ему удовлетворяют, а координаты точки не лежащей на этой поверхности, не удовлетворяют.
О.1.1. Геометрическое место точек  удовлетворяющих уравнению
удовлетворяющих уравнению 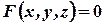 называется поверхностью.
называется поверхностью.
Две задачи, которые ставятся перед аналитической геометрией:
1) зная уравнение поверхности, определить ее вид;
2) зная поверхность, составить уравнение.
При этом поверхности могут быть:
1) первого порядка, если уравнение первого порядка - плоскость;
2) второго порядка, если уравнение второго порядка – поверхность.
Рассмотрим в пространстве плоскость 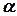 . Её положение вполне определяется заданием вектора
. Её положение вполне определяется заданием вектора 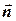 , перпендикулярным данной плоскости и некоторой фиксированной точкой
, перпендикулярным данной плоскости и некоторой фиксированной точкой 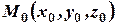 лежащей в плоскости
лежащей в плоскости 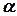 .
.
О.2.1. Вектор 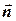 , перпендикулярный плоскости
, перпендикулярный плоскости 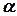 , называется вектором нормали этой плоскости.
, называется вектором нормали этой плоскости.
Если обозначить через 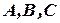 координаты вектора
координаты вектора 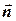 , то
, то 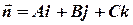 .
.
Выведем уравнение плоскости 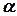 , проходящей через данную точку
, проходящей через данную точку 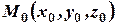 , и имеющей нормальный вектор
, и имеющей нормальный вектор 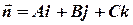 .
.
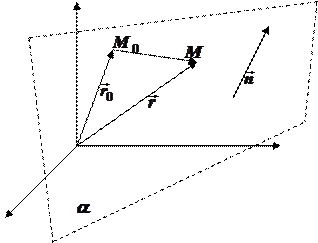 |
Для этого:
1) возьмем произвольную точку 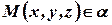 ;
;
2) рассмотрим вектор 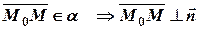 .
.
Следовательно, скалярное произведение
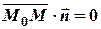 . (2)
. (2)
Из построения 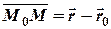 , тогда уравнение (2) примет вид
, тогда уравнение (2) примет вид
 . (3)
. (3)
Уравнение (3) называется векторным уравнением плоскости.
В координатной форме
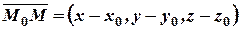 , а
, а 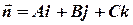 ,
,
тогда получим
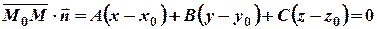 или
или
 (4)
(4)
Уравнение (4) называется уравнением плоскости, проходящей через данную точку.
Пример №1. Написать уравнение плоскости, проходящей через точку 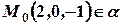 с вектором
с вектором 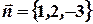 .
.
Решение:  .
.
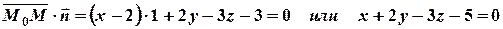
Очевидно, что всякой плоскости соответствует уравнение первой степени относительно текущих координат.
Рассмотрим уравнение (4)
 .
.
Раскроем скобки и преобразуем полученное выражение:
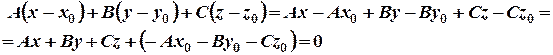
Обозначим через  . Получим уравнение вида
. Получим уравнение вида
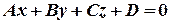 , (5)
, (5)
Уравнение (5) называется общим уравнением плоскости.
Рассмотрим зависимость положение плоскости от коэффициентов.
1) Пусть  Тогда вектор нормали
Тогда вектор нормали 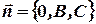 . Если проекция вектора
. Если проекция вектора 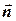 на ось
на ось 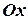 равна нулю, то он проектируется в точку и расположен перпендикулярно оси
равна нулю, то он проектируется в точку и расположен перпендикулярно оси 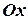 , т.е.
, т.е.  . Следовательно, в этом случае плоскость расположена параллельно той оси, одноименная координата которой отсутствует в уравнении плоскости.
. Следовательно, в этом случае плоскость расположена параллельно той оси, одноименная координата которой отсутствует в уравнении плоскости.
Аналогично.
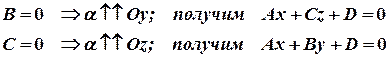
2) Пусть 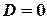 , т.е.
, т.е. 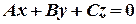 .В этом случае координаты точки О(0.0,0) удовлетворяют уравнению плоскости, следовательно плоскость проходит через начало координат.
.В этом случае координаты точки О(0.0,0) удовлетворяют уравнению плоскости, следовательно плоскость проходит через начало координат.
3) Пусть 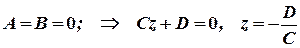 плоскость параллельна координатной плоскости
плоскость параллельна координатной плоскости 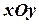 и проходит через точку
и проходит через точку 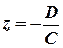
Аналогично:
Если 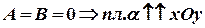 .
.
Если 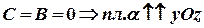 .
.
4) Пусть 
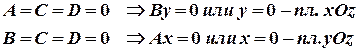
Пусть дана плоскость
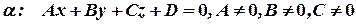 (7)
(7)
На оси 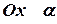 отсекает отрезок равный
отсекает отрезок равный  .
.
На оси отсекает отрезок равный
отсекает отрезок равный  .
.
На оси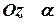 отсекает отрезок равный
отсекает отрезок равный 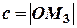 .
.
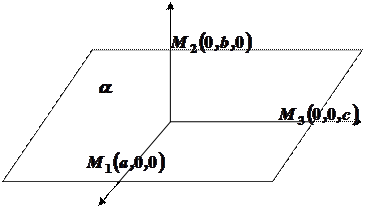
Так как точка 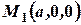 принадлежит плоскости
принадлежит плоскости 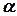 , то ее координаты удовлетворяют уравнению плоскости, тогда получим:
, то ее координаты удовлетворяют уравнению плоскости, тогда получим:
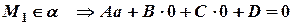 отсюда
отсюда 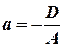
Аналогично
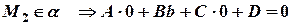 отсюда
отсюда 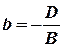 (8)
(8)
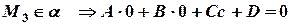 отсюда
отсюда 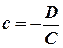 .
.
Пусть 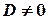 . Разделим уравнение (7) на
. Разделим уравнение (7) на 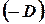 , получим:
, получим:
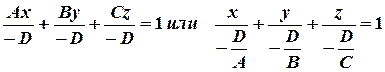 .
.
С учетом равенств (8) уравнение приобретет вид:
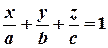 (9)
(9)
Уравнение (9) называется уравнением плоскости в отрезках.
Пусть даны три точки 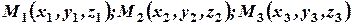 и текущая точка
и текущая точка  . Найдем уравнение плоскости, проходящей через три данные точки. Для этого рассмотрим три вектора, выходящих из одной точки
. Найдем уравнение плоскости, проходящей через три данные точки. Для этого рассмотрим три вектора, выходящих из одной точки 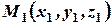 . Найдем координаты этих векторов:
. Найдем координаты этих векторов:
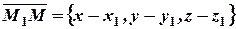
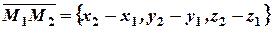
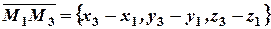 .
.
Так как три точки лежат в одной плоскости, то векторы 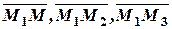 компланарны. Условие компланарности. (смешанное произведение векторов равно нулю). Найдем смешанное произведение найденных векторов:
компланарны. Условие компланарности. (смешанное произведение векторов равно нулю). Найдем смешанное произведение найденных векторов:
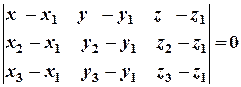 (10).
(10).
Уравнение (10) называется уравнением плоскости, проходящей через три данные точки.
Пусть даны две плоскости:
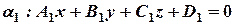
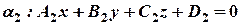
Под углом между двумя плоскостями мы понимаем один из двугранных углов, образованных этими плоскостями. Т.е.
 .
.
Следовательно, используя скалярное произведение векторов, получим:
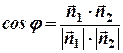 . (11)
. (11)
По условию координаты векторов нормали известны
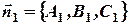 ;
; 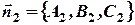 . Тогда в координатной форме (11) примет вид
. Тогда в координатной форме (11) примет вид
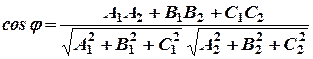 (12)
(12)
Условие перпендикулярности плоскостей: 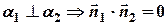 , т.е.
, т.е.
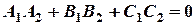 .
.
Условие параллельности плоскостей: 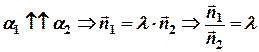 , тогда в координатной форме:
, тогда в координатной форме: 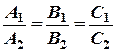
 2014-02-09
2014-02-09 635
635







