СОДЕРЖАНИЕ
6.
Сначала выясним какой угол будем принимать за угол между двумя прямыми на плоскости.
О.6.1. Углом между двумя прямыми 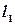 и
и 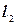 на плоскости называется угол, на который нужно повернуть прямую
на плоскости называется угол, на который нужно повернуть прямую 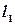 , относительно точки пересечения этих прямых против часовой стрелки, до совпадения с прямой
, относительно точки пересечения этих прямых против часовой стрелки, до совпадения с прямой 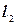 (см. рис.6;
(см. рис.6; 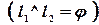 ).
). 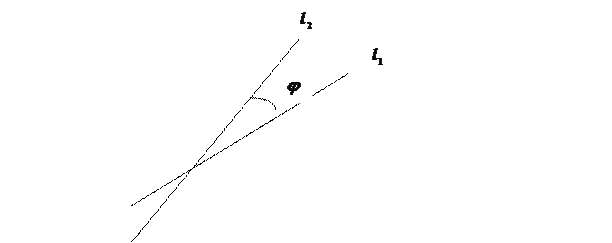
Рисунок 6
Для получения угла между прямой 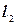 и
и 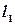 , нужно прямую
, нужно прямую 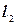 повернуть против часовой стрелки до совпадения с прямой
повернуть против часовой стрелки до совпадения с прямой 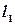 .
.
Построим две прямые 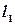 и
и 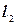 в системе координат на плоскости и угол между ними обозначим через
в системе координат на плоскости и угол между ними обозначим через 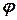 (см. рис7).
(см. рис7).
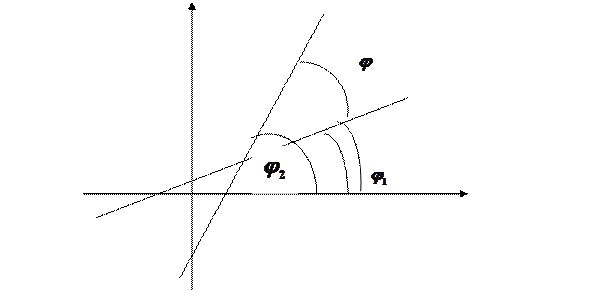
Рисунок 7.
Угол между прямыми 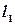 и
и 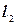 равен
равен 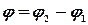 . Тогда
. Тогда 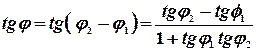 . Так как
. Так как 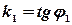 , а
, а 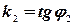 , то
, то 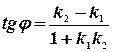 (11)
(11)
Формула (11) определяет угол между двумя прямыми на плоскости.
Рассмотрим условия параллельности и перпендикулярности прямых на плоскости.
1) Пусть прямые 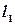 и
и 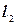 параллельны. Это значит, что угол между ними равен нулю, т.е.
параллельны. Это значит, что угол между ними равен нулю, т.е. 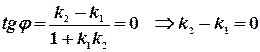 . Отсюда
. Отсюда
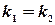 (12)
(12)
Из равенства (12) следует, что если прямые параллельны, то их угловые коэффициенты равны.
Если уравнения прямых заданы в общем виде т.е.
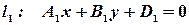
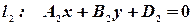 ,
,
то имеем: 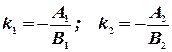 . По условию (12) получим
. По условию (12) получим
|
|
|
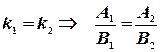 .
.
Это условие параллельности равносильно условию (12).
2) Пусть прямые 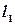 и
и 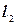 перпендикулярны, тогда
перпендикулярны, тогда 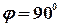 и тангенс этого угла не существует. Тогда возьмем функцию котангенс угла
и тангенс этого угла не существует. Тогда возьмем функцию котангенс угла 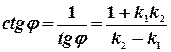 . Известно, что
. Известно, что 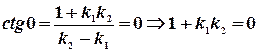 .
.
Отсюда условие перпендикулярности имеет вид: 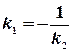 (13)
(13)
Из равенства (13) следует, что если прямые перпендикулярны, то их угловые коэффициенты обратные по величине и противоположны по знаку.
Для общего уравнения прямых условие (13) примет вид:
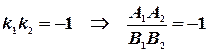 . Отсюда
. Отсюда 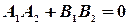 .(напоминает формулу для скалярного произведения векторов).
.(напоминает формулу для скалярного произведения векторов).
Стр.
Список сокращений……………………………………………………………… 5
Введение…………………………………………………………………………… 6
с компьютерной техникой……………………………………………. 7
1.1 Проблематика исследования отрицательного воздействия
компьютеров (7).
1.2 Источники и виды негативных факторов на рабочих местах
с компьютерной техникой (7).
1.3 Краткая характеристика факторов вредности (10).
1.4 Краткая характеристика опасных факторов (16).
1.5 Специфика воздействия негативных факторов (16).
 2014-02-09
2014-02-09 625
625







