2014-02-09
404
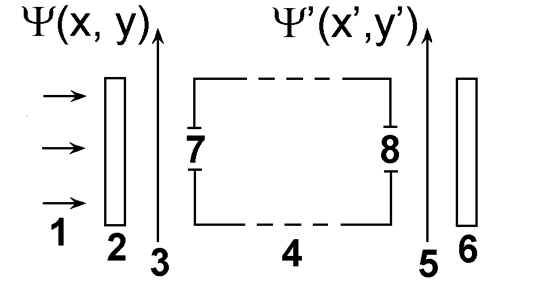
В самом общем виде функциональная схема записи и обработки оптической информации приведена на рис.1.1. Плоская монохроматическая волна 1 освещает объект 2, который размещают во входной (предметной) плоскости системы 3. Излучение, прошедшее объект или отраженное от него, попадает во входное отверстие (входной зрачок) 7 оптической системы 4. Пройдя элементы оптической системы, излучение выходит из выходного отверстия (выходного зрачка) 8 и формирует в выходной плоскости (плоскости изображений) 5 изображение объекта. Вблизи плоскости изображений располагается светочувствительный элемент 6 регистрирующей системы (фотопластина, матрица фотоприемников и т.д.)
В тех случаях, когда оптическая система играет роль оптического процессора, у входной плоскости системы вместо объекта 2 располагается преобразователь входных сигналов. Он, пространственно модулируя падающую на него световую волну, преобразует информацию, поступающую от некоторого источника во входной оптический сигнал. В одном случае преобразователь может представлять собой слайд, на котором информация записана в виде изменяющего коэффициента пропускания. В другом случае в качестве преобразователя может использоваться слой жидкости, рельеф поверхности которой изменяется под действием ультразвуковых волн или электронного пучка.
|
| Рис.1.1.Схема оптической обработки информации. 1-плоская монохроматическая волна; 2-объект; 3-входная (предметная) плоскость; 4-оптическая система; 5-выходная плоскость (плоскость изображения); 6-светочувствительный элемент; 7-входное отверстие (входной зрачок); 8-выходное отверстие (выходной зрачок). |
Свяжем с входной плоскостью оптической системы прямоугольную систему координат (x,y), а с выходной - систему координат (x',y’). Если в системе отсутствуют нелинейные оптические элементы, между входным сигналом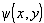 
и выходным сигналом 
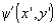(см. рис..1.1) может быть записана в виде
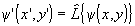, (1.1)
где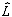 
- некий линейный оператор. Линейность преобразования означает, что выходной сигнал от суммы входных сигналов равен сумме выходных сигналов от каждого входного сигнала в отдельности.
2.ФУРЬЕ-ПРЕОБРАЗОВАНИЕ: ПРЯМОЕ И ОБРАТНОЕ (одномерное и двумерное).
Сделаем небольшое математическое отступление. Многие колебательные и волновые процессы самой различной физической природы при достаточно малых амплитудах могут с высокой точностью считаться гармоническими. Более того, любые сложные колебания всегда можно представить в виде совокупности гармонических составляющих. Эта возможность реализуется как экспериментально с помощью специальных приборов, называемых спектральными анализаторами, так и теоретически с помощью рядов (и интегралов) Фурье. Согласно теореме Ж. Фурье (1822 г.) «любое повторяющееся движение можно рассматривать как результат наложения простых гармонических движений; любую волну независимо от ее формы можно рассматривать как сумму простых гармонических волн». Согласно теории рядов Фурье, всякая периодическая функция f(t), ограниченная на отрезке и имеющая конечное число экстремумов и точек разрыва первого рода (условия Дирихле), может быть представлена в виде тригонометрического ряда:
f(t) = а0 +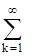 
(ak sin kωt + bk cos kωt), (2.1)
где ω =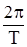 
, T — период функции f(t),
ak =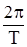 
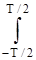f(t) sin kωt dt (2.2)
bk = 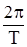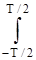f(t) cos kωt dt. (2.3)
Постоянная составляющая ряда Фурье (3.1) а0 является средним значением функции f (t) за период:
a0 =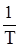 
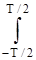f(t) dt (2.4)
Для четной функции (f (-t) = f (t)) все коэффициенты ak равны нулю. Для нечетной (f (-t) = -f (t)) равны нулю коэффициенты а0 и bk.
Таким образом, любое периодическое колебание может быть представлено в виде суммы гармонических колебаний кратных частот ω, 2ω, Зω,...; частота ω называется основной частотой, остальные — гармониками. Количество и амплитуды гармоник тем больше, чем сильнее данное колебание отличается от простого гармонического колебания с частотой ω. Совокупность гармонических составляющих сложного колебания называется его спектром. Нахождение амплитуд и частот гармоник сложного периодического процесса с помощью рядов Фурье носит название гармонического анализа.
Для решения той же задачи могут использоваться комплексные ряды Фурье в виде:
f(t) =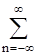 
ane i nωt, (2.5)
где n принимает целочисленные положительные и отрицательные значения в интервале от -∞ до ∞, коэффициенты an выражаются как
an =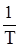 
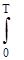f(t) e –inωtd t
В разложении (3.5) представлен дискретный спектр частот:
ω, 2 ω, 3 ω,…, n ω.
Непериодическая функция f(t) представляется в виде комплексного интеграла Фурье:
f(t) =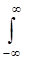 
a( ω )e iωtd ω, (2.6)
являющегося обобщением ряда Фурье на случай непрерывного спектра частот: - ¥-< ω < ¥. Амплитудная функция a( ω ) выражается как:
a( ω ) =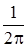 
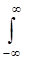f(t) e-iωtdt (2.7)
Иначе, выражение (3.7) называется преобразованием Фурье или фурье-образом (а также спектром Фурье, частотным спектром) функции f(t). Обратное преобразование Фурье функции a( ω ) определяется выражением (3.6). Заметим, что математические операции прямого и обратного преобразований отличаются только знаком экспоненты в подынтегральном выражении.
Рассмотрим теперь комплексную функцию g двух независимых переменных х и у. Тогда двумерное преобразование Фурье F(g) записывается в виде:
F(g)=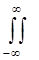
g(x,y) e-i(
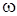x
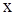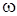+y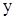
)dxdy (2.8)
Преобразование такого вида представляет собой функцию двух независимых переменных ωХ и ωY, которые мы обычно называем пространственными частотами. Обратное преобразование Фурье функции G(ωx, ωy) определяется формулой:
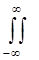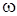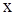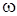F -1(G)=G(ωx, ωy) ei(x+y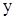)dωx dωy (2.9)
