Коэффициент вариации. До сих пор мы изучали показатели, которые были выражены в абсолютных величинах, то есть в тех же именованных числах

До сих пор мы изучали показатели, которые были выражены в абсолютных величинах, то есть в тех же именованных числах, что и варьирующий признак (в данном примере — в килограммах).

Однако квадратическое отклонение, как и всякая абсолютная величина, недостаточно наглядно характеризует колеблемость вариант вокруг средней величины.

О том, насколько велико это отклонение, можно судить только при расчете коэффициента вариации.

Коэффициент вариации представляет собой отношение среднего квадратического отклонения к средней арифметической и выражается в процентах.

Коэффициент вариации рассчитывается по формулам:

а) для среднего квадратического отклонения (простого):

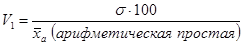
и в нашем примере составит:

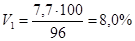
б) для среднего арифметического отклонения (взвешенного):

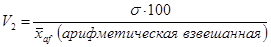
т.е.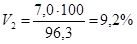

Коэффициент вариации является отвлеченным числом и по­этому он наиболее удобен в измерении вариации признаков.

Кроме того, этот показатель можно использовать для сравнения колеблемости совокупностей как с одинаковыми, так и с различны­ми признаками.

Пример. Предположим, что мы определяем колеблемость веса одной кипы шерсти по двум партиям путем сравнения коэффициен­тов вариации I и II партий. Это будет сравнение колеблемости сово­купностей, имеющих одинаковые признаки. Или, например, требу­ется сравнить, что больше колеблется: средний объем товарооборо­та одной торговой фирмы или средний размер площади торгового зала, то есть сравниваем совокупности с разными признаками и оп­ределяем степень колеблемости этих различных признаков путем вычисления коэффициентов вариации.