Задание
 Исследуйте функцию на основе ее графика.
Исследуйте функцию на основе ее графика.
Используйте двухэтажные записи для обозначения взаимосвязанных утверждений.
II. Элементарные функции (аналитическая запись; график; свойства).
| № | Аналитическая запись | График | Свойства | |
| 1. | у = kx + b – линейная функция | 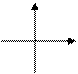 k > 0; b > 0 k > 0; b > 0
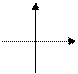 k > 0; b < 0 k > 0; b < 0
| 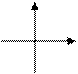 k < 0; b > 0 k < 0; b > 0
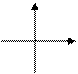 k < 0; b < 0 k < 0; b < 0
| 1. D (y) = … 2. Е (y) = … 3. y = 0 при … |
| k > 0 4. Возрастает на D (y). 5. у > 0 при х ….; у < 0 при х … | k < 0 4. Убывает на D (y). 5. у > 0 при х ….; у < 0 при х … | |||
| 6. Если b = 0, то функция нечетная | ||||
k = 0; b > 0
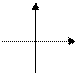
| 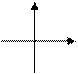 k = 0; b < 0 k = 0; b < 0
| |||
| 2. | у = аx 2 + bx + с – квадратичная функция | 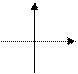 a > 0; D > 0 a > 0; D > 0
| 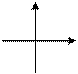 a < 0; D > 0 a < 0; D > 0
|  Определить знаки коэффициентов, дискриминанта; описать свойства
Определить знаки коэффициентов, дискриминанта; описать свойства
|
a > 0; D < 0
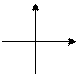
| a < 0; D < 0
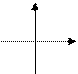
| |||
 a > 0; D = 0 a > 0; D = 0
|  a < 0; D = 0 a < 0; D = 0
| |||
| 3. | у =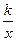 – функция обратной пропорциональности – функция обратной пропорциональности
| 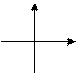 k > 0 k > 0
|  k < 0 k < 0
| 1. D (y) = … 2. Е (y) = … 3. y ¹ 0 при любом x из D (y) 4. Если k > 0 – функция ……….., k < 0 – функция ……………… при х Î (…., ….) и х Î (…., ….) 5. Если k > 0, то у > 0 при х ….; у < 0 при х … если k < 0, то у > 0 при х ….; у < 0 при х … 6. Функция нечетная |
| 4. | у = хп – степенная функция при п ÎN | 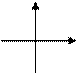 п – четное п – четное
| 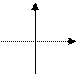 п – нечетное п – нечетное
| п – четное 1. D (y) = … 2. Е (y) = … 3. y = 0 при … 4. Возрастает при…. | п – нечетное 1. D (y) = … 2. Е (y) = … 3. y = 0 при … 4. Возрастает при…. | ||
| 5. | у =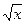
| 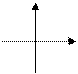
| 1. D (y) = … 2. Е (y) = … 3. y = 0 при … 4. Возрастает при…. | ||||
| 6. | у = ах – показательная функция |  a > 1 a > 1
| 0 < a < 1
| 1. D (y) = … 2. Е (y) = … 3. y ¹ 0 при любом x из D (y) | |||
| a > 1 4. Возрастает при…. | 0 < a < 1 4.Убывает при…. | ||||||
| 7. | у = logax – логарифмическая функция |  a > 1 a > 1
| 0 < a < 1
| 1. D (y) = … 2. Е (y) = … 3. y = 0 при x = … | |||
| a > 1 4. Возрастает при…. | 0 < a < 1 4.Убывает при…. | ||||||
| 5. у > 0 при х ….; у < 0 при х … | 5. у > 0 при х ….; у < 0 при х … |
 2014-02-09
2014-02-09 257
257