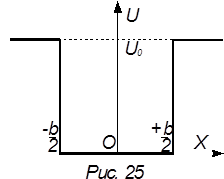 Рассмотрим более сложную задачу: частица находится в связанном состоянии в потенциальной яме, борта которой имеют конечную высоту U0. Понятно, что состояние будет связанным только в том случае, когда полная энергия частицы меньше высоты потенциального барьера. Ситуация отличается от выше рассмотренной. Во-первых тем, что вследствие квантового туннелирования волновая функция вне ямы не равна нулю. Второе принципиальное отличие состоит в том, что скачок потенциала на границе ямы имеет не бесконечную, а конечную величину. Проведение анализа дифференциального уравнения для пространственной составляющей волновой функции, аналогичное проделанному выше, приводит к выводу, что на границах ямы не только сама волновая функция непрерывна, но непрерывна также ее производная по координате. Самая большая неоднородность производной волновой функции в этих точках – изломы.
Рассмотрим более сложную задачу: частица находится в связанном состоянии в потенциальной яме, борта которой имеют конечную высоту U0. Понятно, что состояние будет связанным только в том случае, когда полная энергия частицы меньше высоты потенциального барьера. Ситуация отличается от выше рассмотренной. Во-первых тем, что вследствие квантового туннелирования волновая функция вне ямы не равна нулю. Второе принципиальное отличие состоит в том, что скачок потенциала на границе ямы имеет не бесконечную, а конечную величину. Проведение анализа дифференциального уравнения для пространственной составляющей волновой функции, аналогичное проделанному выше, приводит к выводу, что на границах ямы не только сама волновая функция непрерывна, но непрерывна также ее производная по координате. Самая большая неоднородность производной волновой функции в этих точках – изломы.
Граничные условия, которым должна удовлетворять волновая функция должны иметь вид:
y(– 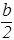 –0)=y(–
–0)=y(– 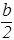 +0), y`(–
+0), y`(– 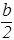 –0)=y`(–
–0)=y`(– 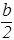 +0)=0, (32)
+0)=0, (32)
y(+ 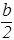 –0)=y(+
–0)=y(+ 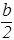 +0), y`(+
+0), y`(+ 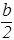 –0)=y`(+
–0)=y`(+ 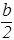 +0). (33)
+0). (33)
Как и раньше, частица внутри потенциальной ямы свободна, поэтому в области – b/2<x<b/2 волновая функции должна описываться законом косинуса или синуса. Вне потенциальной ямы волновая функция удовлетворяет уравнению:
Ey=– 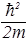
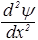 +U0y Þ
+U0y Þ 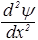 –
– 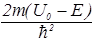 y=0. (34)
y=0. (34)
Нетрудно увидеть, что при E<U0 решением уравнения (34) является функция
y(x)=q×e-ax, (35)
где
a= 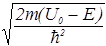 =
= 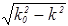 . (36)
. (36)
Волновое число k имеет тот же смысл, что и в разделе 1.1, а
k 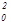 =
= 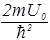 . (37)
. (37)
Используем граничные условия в точке x=b/2. Имеем
a×cos 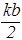 =q×e-a
=q×e-a 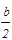 , (38)
, (38)
ak×sin 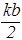 =–qa×e-a
=–qa×e-a 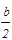 , (39)
, (39)
Если поделим почленно уравнение (39) на уравнение (38), то получим:
k×tg 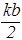 =a Þ k×tg
=a Þ k×tg 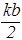 =–
=– 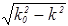 . (40)
. (40)
Решение уравнения (40) дает допустимые значения волнового числа k.
 Графическая схема решения уравнения (40) показана на рисунке 26. График зависимости правой части от k представляет собой нижнюю полуокружность радиуса k0, а график левой части имеет много ветвей. Точки пересечения графиков левой и правой частей уравнения дают возможные значения волнового числа. Решения, дающие малые значения волнового числа довольно близки к тому, что получаются для частицы в бесконечно глубокой потенциальной яме (в рассматриваемой ситуации окружность имела бы бесконечный радиус. Она бы пересекала тангенсоподобные ветви в асимптотике kb=p. Чем больше k, т.е. чем ближе значения полной энергии частицы к высоте бортов потенциальной ямы, тем сильнее отклонения значений k от результатов расчетов, даваемых моделью бесконечно глубокой потенциальной ямы. Последние уровни могут находиться довольно близко друг от друга. Число энергетических уровней ограничено.
Графическая схема решения уравнения (40) показана на рисунке 26. График зависимости правой части от k представляет собой нижнюю полуокружность радиуса k0, а график левой части имеет много ветвей. Точки пересечения графиков левой и правой частей уравнения дают возможные значения волнового числа. Решения, дающие малые значения волнового числа довольно близки к тому, что получаются для частицы в бесконечно глубокой потенциальной яме (в рассматриваемой ситуации окружность имела бы бесконечный радиус. Она бы пересекала тангенсоподобные ветви в асимптотике kb=p. Чем больше k, т.е. чем ближе значения полной энергии частицы к высоте бортов потенциальной ямы, тем сильнее отклонения значений k от результатов расчетов, даваемых моделью бесконечно глубокой потенциальной ямы. Последние уровни могут находиться довольно близко друг от друга. Число энергетических уровней ограничено.
Несомненный интерес представляет вид распределений амплитуд вероятности в стационарных состояниях. Для примера получим вид волновых функций частицы для основного и следующего за ним по энергии состояний. Пусть k0=4 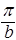 . Значения волнового числа, отвечающего этим двум состояниям, будут мало отличаться от того, что получается при бесконечно глубокой потенциальной яме, т.е. в нулевом приближении можно положить, что k1=
. Значения волнового числа, отвечающего этим двум состояниям, будут мало отличаться от того, что получается при бесконечно глубокой потенциальной яме, т.е. в нулевом приближении можно положить, что k1= 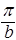 , k2=2
, k2=2 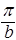 . Тогда
. Тогда
a1= 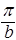
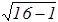 »3,88
»3,88 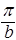 , a2=
, a2= 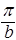
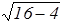 »3,5
»3,5 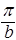 . (41)
. (41)
Определим поправки к волновому числу. Для нулевого уровня имеем:
k×tg 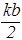 =–
=– 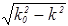 Þ
Þ 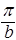 ×tg
×tg 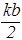 »–3,88
»–3,88 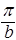 , Þ tg
, Þ tg 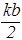 »–3,88. (42)
»–3,88. (42)
Понятно, что из (42) следует, что произведение kb близко к значению p. А так как
tg 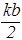 =
= 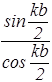 »
» 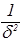 sin
sin 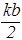 »–
»– 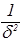 , (43)
, (43)
где d – отклонение величины kb/2 от значения p /2.
 2014-02-09
2014-02-09 2147
2147
