Частица в трехмерной потенциальной яме

В реальном мире частицы совершают движение в трехмерном пространстве. Эвристический вывод уравнения Шредингера применительно к движению амплитуд вероятности в трехмерном пространстве можно сделать аналогично проведенному выше анализу. Уравнение Шредингера при этом принимает вид:

iћ 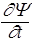= 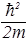( 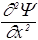+ + 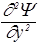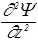)+U(x,y,z)Y, (44)

или

iћ 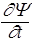= 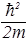ѲY+U(x,y,z)Y, (45)

Повторим описание состояний частицы в случае трехмерной бесконечно глубокой потенциальной ямы. Положим, что яма имеет форму куба с ребром равным b и частица не может проникнуть сквозь стенки ямы.

Процедура описания состояний в общих чертах повторяет описание одномерной ситуации. Опишем стационарные состояния. В стационарном состоянии зависимость волновой функции от времени имеет вид:

Y(x, y, z, t)=y(x, y, z)×exp{–i 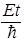}. (46)

Подстановка данной зависимости в уравнение (45) дает:

Ey=– 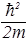( 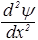+ + 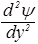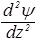)+Uy. (47)

Необходимо найти зависимость y(x, y, z) внутри ямы, где U=0. Техника решения уравнения (47) содержит новый элемент – разделение переменных. В основе метода лежит предположение, что функция y(x, y, z) представляет собой произведение трех функций, каждая из которых зависит только от одной координаты:

y(x, y, z)=X(x)Y(y)Z(z). (48)

После подстановки данного пробного решения в (55) получаем:

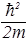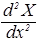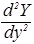E X×Y×Z=– (Y×Z +X +X×Y 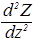). (49)

Поделим обе части уравнения (49) на X×Y×Z, тогда оно приведется к такому виду:

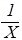
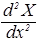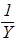
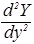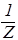
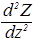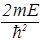+ + =– . (50)

В уравнении (50) содержится одна важная идея. Каждое из слагаемых в левой части уравнения (50) зависит только от одной переменной. Их сумма равна постоянной величине. В силу независимости слагаемых можно сделать вывод, что такое возможно только при условии, что каждое слагаемое равно постоянной величине. Для унификации и придания большей физической осмысленности математической процедуре, обозначим эти постоянные через – 2mEx/ћ², –2mEy/ћ², – 2mEz/ћ². Их сумма должна равняться правой части уравнения (50), т.е. – 2mE/ћ². Итак, получаем три уравнения:

=–,

=–,

=–,

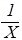
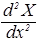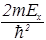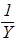
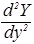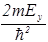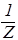
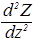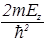которые можно переписать в более знакомом виде:

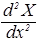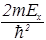+ X = 0, (51)

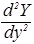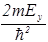+ Y=0, (52)

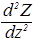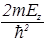+ Z=0. (53)

Таким образом, мы пришли к трем уже решенным ранее задачам. Каждое решение: X(x), Y(y), Z(z) характеризуется своим волновым числом, через которое выражаются постоянные Ex, Ey, Ez:

kx= 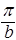nx; ky= 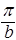ny; kz= 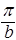nz, (54)

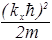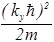Ex= ; Ey= ; Ez= 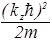. (55)

Целые числа nx, ny, nz являются квантовыми числами состояния частицы. Они являются полными характеристиками стационарного состояния (можно сказать, являются полным именем состояния: “Эн-икс Эн-игрекович Эн-зетов”). Квантовые числа дают энергетический спектр частицы:

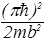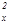E=Ex+Ey+Ez= (n 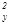+n +n 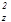). (56)

Полная волновая функция частицы в яме имеет вид:

Y(x, y, z, t)=a×sin kxx×sin kyy×sin kzz exp{–i 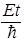}, (57)

Y(x, y, z, t)=a×cos kxx× cos kyy× cos kzz exp{–i 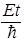}. (58)

Это стоячая волна амплитуды вероятности.