Проведем анализ на примере первой схемы – АГ с индуктивной ОС.
Первое условие: ПОС
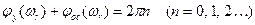
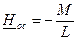
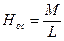
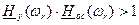
Найдем 2 условия нахождения, исходи из того, что нужно чтобы после включения генератора, имеющиеся шумовые колебания нужной частоты ω, увеличивались по амплитуде.
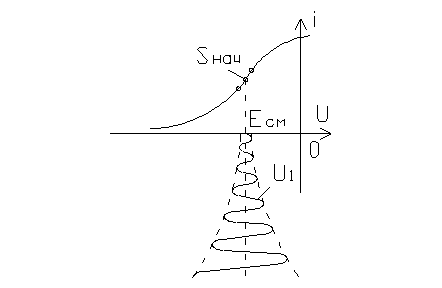
Так как в момент возбуждения генератора амплитуда действующих там колебаний мала, то можно считать транзистор линейным элементом, а сам генератор линейной цепью, описываемой линейным уравнением.
Заменим схему генератора эквивалентной схемой по переменному току.
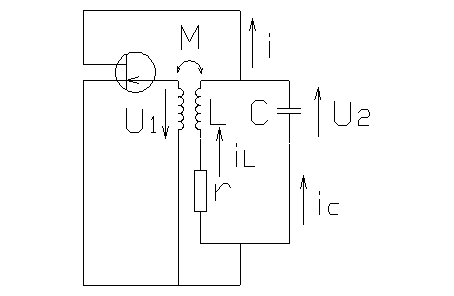
Составим ДУ
(1) 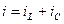 , где
, где 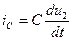 (2)
(2)
(3) 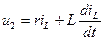
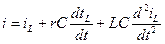 (4)
(4)
С другой стороны, ток протекающий через транзистор находится в соответствии с выражением (5)
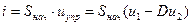 , где
, где 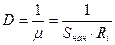
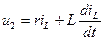
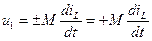
М – коэффициент взаимной индуктивности
(6) 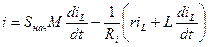
Приравняем (4) и (6)
(7) 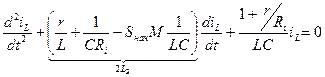
(8) 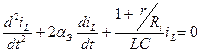
Характеристическое уравнение:
(9) 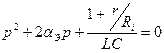
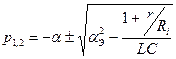
(10) 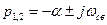 , где
, где 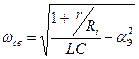 – частота свободных колебаний в контуре.
– частота свободных колебаний в контуре.
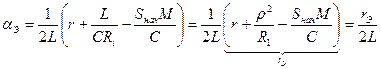
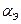 – коэффициент затухания эквивалентного контура с учетом собственных потерь r и потерь, вносимых в контур за счет выходного сопротивления транзистора Ri и ОС.
– коэффициент затухания эквивалентного контура с учетом собственных потерь r и потерь, вносимых в контур за счет выходного сопротивления транзистора Ri и ОС.
rэ – результирующие потери эквивалентного контура.
В теории линейных цепей получено условие устойчивости линейной цепи – условие устойчивости состояния покоя: если цепь выведена из состояния покоя каким-то внешним воздействием, то после прекращения этого воздействия цепь должна вернуться в прежнее состояние, то есть свободные колебания в цепи должны быть затухающими. Для этого действительная часть всех корней характеристического уравнения, описывающего цепь должна быть отрицательной. В генераторе же наоборот требуется обеспечить неустойчивость, то есть чтобы линейная цепь стала генератором или возбудилась, нужно чтобы действительная часть всех корней характеристического уравнения должна быть положительной.
Из выражения (10) 2 условия:
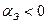 (11)
(11)
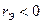
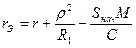
если 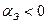 , то
, то 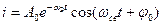
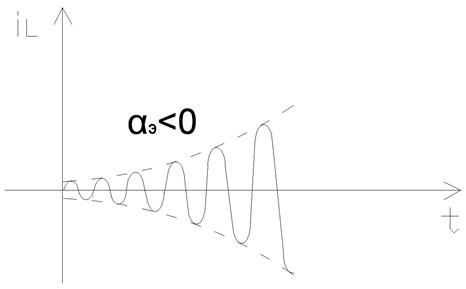
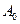 и
и 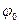 определяются начальными условиями
определяются начальными условиями
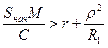
(12) 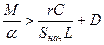 ,
, 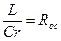
(13) 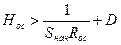
(14) 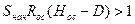
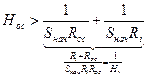
(15) 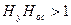
Полученное выражение для второго условия возбуждения генератора справедливы для всех трех электрических схем.
Вывод: для возбуждения LC-АГ с внешней ОС необходимо одновременно выполнение двух условий:
- баланса фаз 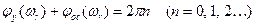
- 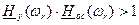 .
.
 2014-02-09
2014-02-09 579
579








