2014-02-09
652
Разобьем интервал интегрирования на четное число отрезков. Рассмотрим сдвоенный участок [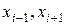
]. Заменим исходную подынтегральную функцию квадратичнойпараболой. Построим параболу
,
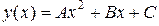принимающую в точках
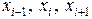
значения (см. рис. 3.5.4)
, 
, 
.
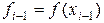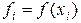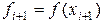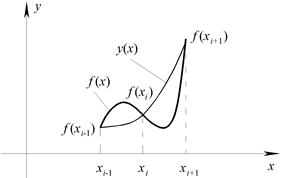
Рис. 2.5.4. К интегрированию по формуле Симпсона.
Такая парабола может быть представлена формулой
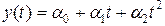, (2.5.13)
где
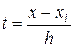, при этом 
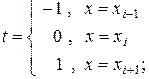(2.5.14)
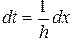или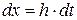 
. (2.5.15)
Делая замену переменных, вычислим приближенное значение интеграла
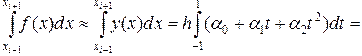
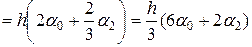
Параметры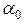 
, 
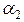определим из условий
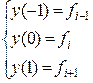
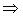
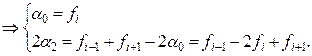
В итоге получим квадратурную формулу Симпсона
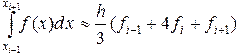. (2.5.16)
Общая формула для вычисления приближенного значения интеграла примет вид
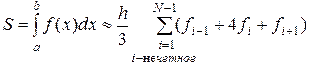. (2.5.17)
Суммирование ведется только по нечетным i. Если перегруппировать члены суммы, получим
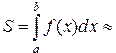
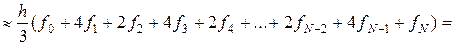
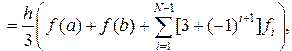
т.е.
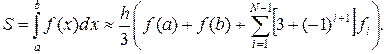(3.5.18)
Точность вычисления. Как следует из построения квадратурные формулы Симпсона дают точный результат интегрирования для функций, имеющих вид квадратичной параболы на сдвоенном участке [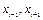
] (
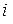– нечетное). При этом одинаковая длина сдвоенных участков вовсе не обязательна и использовалась здесь исключительно для упрощения промежуточных выкладок и вида результирующих формул (2.5.17)–(2.5.18).
В том случае, когда сдвоенные участки имеют одинаковую длину, т.е.
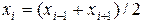– средняя точка сдвоенного участка,
формула Симпсона точна для функций, имеющих вид кубической параболы на этих участках. Это утверждение достаточно проверить для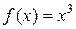 
.
При точном интегрировании имеем:
,
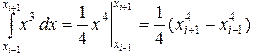а при интегрирование по формуле Симпсона получаем:
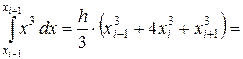
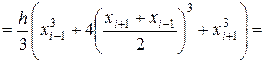
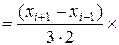
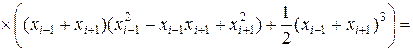
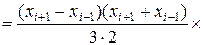
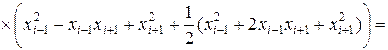
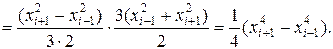
Как видно, результаты точного и численного интегрирования совпадают.
