Заменяем на i -ом участке интегрируемую функцию линейной функцией 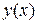 , принимающей в точках
, принимающей в точках 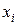 и
и 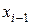 значения (рис. 2.5.3):
значения (рис. 2.5.3):
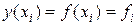 ,
, 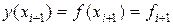 . (2.5.9)
. (2.5.9)
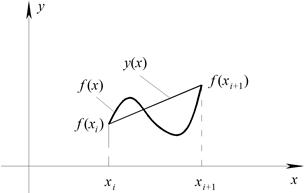
Рис. 2.5.3. К интегрированию по формуле трапеций.
Тогда интеграл на отрезке заменятся площадью трапеции (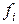 и
и 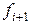 – основания,
– основания, 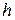 – высота)
– высота)
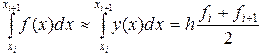 . (2.5.10)
. (2.5.10)
Вычисление исходного интеграла сводится к вычислению суммы
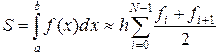 , (2.5.11)
, (2.5.11)
или
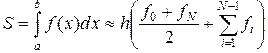 . (2.5.12)
. (2.5.12)
Точность вычисления. Как следует из построения квадратурная формула трапеций дает точный результат интегрирования для функций, линейных на i -ом участке (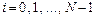 ).
).
 2014-02-09
2014-02-09 551
551








