Пример численного интегрирования полинома

Вычислить

,

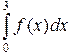где .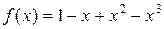

Здесь 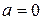и .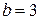

Пусть 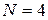, тогда .

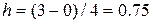Метод прямоугольников.

Имеем: , , .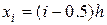

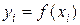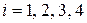Расчет сведен в табличную форму.

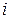
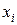
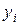
	0.375	0.713
	1.125	–0.283
	1.875	–3.951
	2.625	–12.822

На основании данных, приведенных в таблице, вычисляем приближенное значение интеграла по формуле средних прямоугольников (2.5.6):

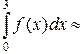0.75·[0.713+(–0.283)+(–3.951)+(–12.822)]=–12.258

Метод трапеций.

Имеем: , , .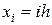

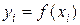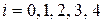Расчет сведен в табличную форму

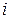
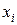
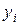
	0.0	1.0
	0.75	0.391
	1.5	–1.625
	2.25	–7.578
	3.0	–20.0

На основании данных, приведенных в таблице, вычисляем приближенное значение интеграла по формуле трапеций (2.5.12):

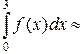0.75·{[1.0+(–20.0)]/2+0.391+(–1.625)+(–7.578)}=–13.734

Метод Симпсона.

Аналогично методу трапеций:

, , .

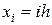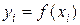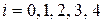Расчет сведен в табличную форму (таблицы метода трапеций и метода Симпсона совпадают).

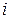
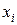
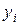
	0.0	1.0
	0.75	0.391
	1.5	–1.625
	2.25	–7.578
	3.0	–20.0

На основании данных, приведенных в таблице, вычисляем приближенное значение интеграла по формуле Симпсона (3.5.18):

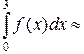0.75/3·[1.0+4·0.391+2 (–1.625)+4 (–7.578)+(–20.0)]=-12.749