Пусть дана СЛАУ порядка 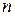 относительно
относительно 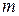 неизвестных:
неизвестных:
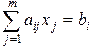 ,
, 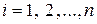 (2.7.11)
(2.7.11)
и при этом количество неизвестных меньше количества уравнений: 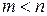 . В общем случае, такая система является несовместной и не имеет точного решения. Тогда можно найти оптимальное решение, т.е. такое, при котором сумма
. В общем случае, такая система является несовместной и не имеет точного решения. Тогда можно найти оптимальное решение, т.е. такое, при котором сумма
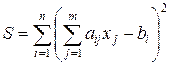 (2.7.12)
(2.7.12)
достигает своего минимума.
Сумма 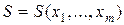 – функция
– функция 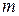 переменных. Для определения точки минимума
переменных. Для определения точки минимума 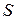 (оптимального решения) повторяем аналогичные выкладки из пункта 2.7.1:
(оптимального решения) повторяем аналогичные выкладки из пункта 2.7.1:
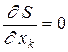
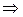
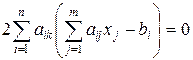 .
.
Меняя порядок суммирования, получим СЛАУ относительно оптимальных значений 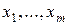 :
:
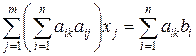 ,
, 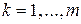 (2.7.13)
(2.7.13)
или в векторно-матричной форме:
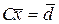 , (2.7.14)
, (2.7.14)
где коэффициенты матрицы и компоненты вектора правой части системы вычисляются по формулам
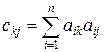 , ,  ; ; | (2.7.15) |
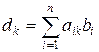 , , 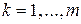 |
Или
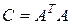 ;
; 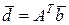 . (2.7.16)
. (2.7.16)
Пример 3.7.1. Пусть требуется найти оптимальное решение системы уравнений
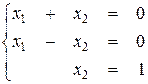
Составим систему уравнений относительно оптимального решения

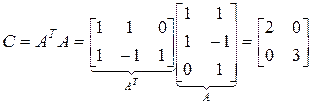 ;
;
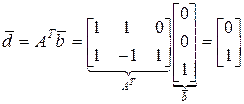 ;
;
Полученная система имеет вид
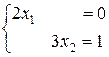
Решением этой СЛАУ (оптимальным решением исходной СЛАУ) будут следующие значения: 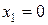 ,
, 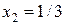 .
.
 2014-02-09
2014-02-09 4002
4002