Аксиома 5

Вероятность произведения событий А · В (или вероятность их одновременного осуществления) равна произведению вероятности одного из них на условную вероятность другого события, вычисленную в предположении, что первое событие произошло.

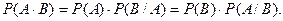
Аксиома 5 может быть распространена на произведегние любого конечного числа событий.

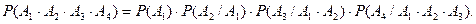
Следствие 1. Пусть событие А не зависит от события В (Р(А)=Р(А/В)).

Тогда из аксиомы 5 будем иметь:

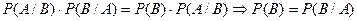- событие В не зависит от А. Другими словами, зависимость и независимость двух событий – взаимная.

Следствие 2. Если событие А не зависит от события В, то из аксиомы 5 получим: 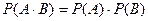. Вероятность произведения независимых событий равна произведению вероятностей эьтих событий.

Примеры. 1) В урне 10 шаров = 4 черных + 6 белых.

Наудачу по одному извлекаем два шара. Какова вероятность, что оба черные?

А: первый шар черный; .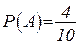

В: второй шар черный, если первый черный P(B/A)=.

С: Оба шара черные;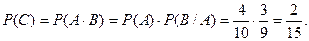

Здесь события А и В зависимые.

2) В урне 10 шаров = 4 черных + 6 белых.

Три раза подряд извлекаем по одному шару, предварительно возвращая вынутый шар в урну. Какова вероятность, что все шары черные?

А: первый шар черный; В: второй шар черный; С: третий шар черный.

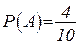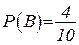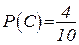; ; . События А, В, С независимые.

D: все извлеченные шары черные; . .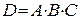

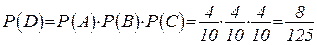Теорема. Вероятность появления суммы двух совместных событий А и В равна сумме вероятностей этих событий без вероятности их совместного появления: .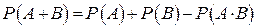

Доказательство (см. рис 4).

1) 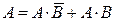, причем события 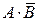и 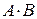несовместные

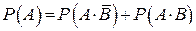
2) 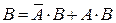, причем события 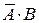и 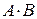несовместные

.

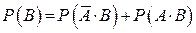3) 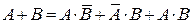, причем события 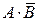, 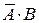и 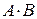несовместные

.

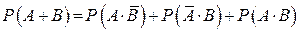из (1)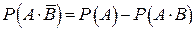

из (2)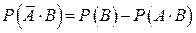

Следовательно, .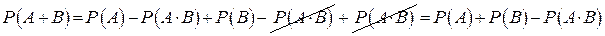

Пример: Вероятность попадания в цель при стрельбе из первого и второго орудий Р₁ = 0,7; Р₂ = 0,8. Найти вероятность попадания в цель при одном залпе хотя бы одним из орудий.

Событие А – попадание в цель первым орудием, В – попадание в цель вторым орудием независимые совместные события.

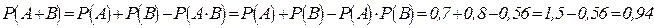Замечание: Аксиома 5 умножения и теорема сложения могут быть доказаны только для классической вероятности (схема случаев). При строгих построениях курса, их принимают в качестве аксиом, полная система которых была сформулирована в 1936 г. академиком А.Н. Колмагоровым.