Пусть имеем множество n однородных элементов. Комбинаторика изучает возможности составления и подсчета количества комбинаций, которые можно составить из элементов исходной группы, и подчиняющихся определенным условиям. Комбинации элементов по-другому называются соединениями.
1) Пусть все элементы исходной группы участвуют в создании комбинаций, 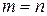 , где m – количество элементов в комбинации.
, где m – количество элементов в комбинации.
Пример Найти количество последовательностей номеров из цифр 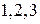 .
.
Получим следующие комбинации: 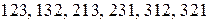 . (6 шт.)
. (6 шт.)
Комбинации отличаются одна от другой только порядком следования элементов. Такие комбинации называются ПЕРЕСТАНОВКИ, обозначаются Рn и количество всех перестановок из n элементов равно 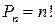 ;
; 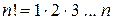 .
.
В примере n = 3; 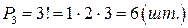 .
.
2) Пусть не все элементы исходной группы участвуют в создании комбинаций, 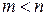 .
.
Пример1 Составить все возможные отношения из трех чисел а, в, с по два числа (без повтора элементов).
Получим следующие комбинации: 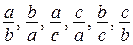 . Их 6 шт. и они отличаются одна от другой или элементами, или порядком их следования, или тем и другим. Такие комбинации называются РАЗМЕЩЕНИЯ, обозначаются
. Их 6 шт. и они отличаются одна от другой или элементами, или порядком их следования, или тем и другим. Такие комбинации называются РАЗМЕЩЕНИЯ, обозначаются 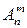 и количество всех размещений из n элементов по m равно
и количество всех размещений из n элементов по m равно
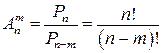
В примере 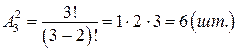 .
.
Пример2 Составить все возможные произведения из трех чисел по два числа (без повтора элементов).
Получим комбинации 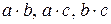 . Их 3 шт. и они отличаются одна от другой только самими элементами, порядок не важен.
. Их 3 шт. и они отличаются одна от другой только самими элементами, порядок не важен.
Такие комбинации называются СОЧЕТАНИЯ, обозначаются 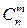 и количество всех сочетаний из n элементов по m равно
и количество всех сочетаний из n элементов по m равно 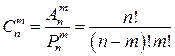 .
.
Важное свойство сочетаний 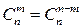 , отсюда
, отсюда 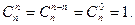
В примере 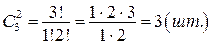 .
.
3) Правило произведения
Пусть имеем множество элементов 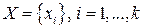 и множество
и множество 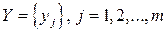 .
.
Один элемент 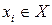 можно выбрать k способами элемент уi Î У можно выбрать т способами. Тогда пару элементов
можно выбрать k способами элемент уi Î У можно выбрать т способами. Тогда пару элементов 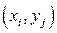 одновременно можно выбрать
одновременно можно выбрать 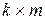 способами: каждый хi сочетается с каждым yj.
способами: каждый хi сочетается с каждым yj.
Пример Из города А в город В можно добраться самолетом и поездом, из В в С – автобусом, поездом и пароходом. Сколько различных возможностей (маршрутов) добраться из города А в город С?
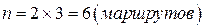 .
.
 2014-02-09
2014-02-09 903
903








