Простейшей системой корреляционной связи является линейная связь между двумя признаками – парная линейная корреляция. Измерение парных корреляций составляет необходимый этап в изучении сложных, многофакторных связей.
Внимание к линейным связям вызвано ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связей для выполнения расчетов преобразуют в линейную форму.
Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:
Ŷ = a+bx,
где ŷ – среднее значение результативного признака у при определенном значении факторного признака х;
а – свободный член уравнения;
b – коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – вариация у, приходящаяся на единицу вариации х.
построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют Метод наименьших квадратов (МНК) МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических ŷ минимальна,т.е.
 å(y – ŷ)2 min
å(y – ŷ)2 min
Система нормальных уравнений:
 na + bå x = å y
na + bå x = å y
aå x + bå x2 = å xy
Можно решить эту систему уравнений по исходным данным или использовать формулы, вытекающие из этой системы:
a = 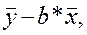
b=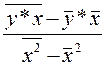 ,
,
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции  rxy для линейной регрессии
rxy для линейной регрессии
(-1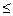 rxy
rxy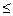 1);
1);
 rxy=
rxy=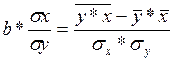 ,
,
 и индекс корреляции r xy – для нелинейной регрессии (0
и индекс корреляции r xy – для нелинейной регрессии (0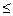 r xy
r xy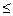 1):
1):
rxy=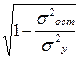 =
=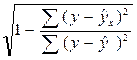 .
.
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
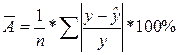
Допустимый предел значений 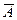 – не более 8 – 10%.
– не более 8 – 10%.
Средний коэффициент эластичности 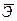 показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения:
показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения:
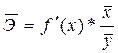 .
.
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
å(yi - 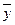 )2 = å(ŷx -
)2 = å(ŷx -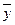 )2 + å(yi - ŷx)2
)2 + å(yi - ŷx)2
где å(yi -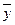 )2 – общая сумма квадратов отклонений – общая дисперсия;
)2 – общая сумма квадратов отклонений – общая дисперсия;
å(ŷx -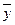 )2 – сумма квадратов отклонений, обусловленная регрессией (это объясненная или факторная дисперсия)
)2 – сумма квадратов отклонений, обусловленная регрессией (это объясненная или факторная дисперсия)
å(yi - ŷx)2 – остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y характеризует коэффициент (индекс) детерминации R2;
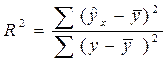 .
.
F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Любая сумма квадратов отклонений связана с числом степеней свободы, которое зависит от числа единиц совокупности n и число определяемых по ней констант (переменных при х)(m).
Dобщ= å(yi - 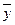 )2 / (n-1)
)2 / (n-1)
Dфакт= å(ŷx -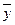 )2 / m
)2 / m
Dост= å(yi - ŷx)2 /(n-m-1)
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия:
F = Dфакт/Dост = 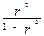 * (n-2)
* (n-2)
где F-критерий для проверки нулевой гипотезы Но: Dфакт = Dост.
Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности (a) наличия нулевой гипотезы (уровень значимости a - вероятность отвергнуть правильную гипотезу при условии, что она верна). Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл – Но отклоняется.
Если эта величина окажется меньше табличного, то вероятность нулевой гипотезы выше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной ошибки:
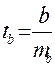 ;
; 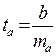 ;
; 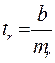
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
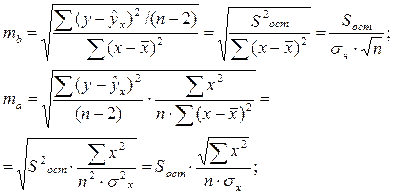
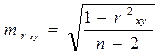
сравнивая фактическое и критическое (табличное) значения t-статистики принимаем или отвергаем гипотезу Но.
Если tтабл < tфакт, то Но отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если tтабл > tфакт, то гипотеза Но не отклоняется и признается случайная природа формирования a, b, r.
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
∆a = tтабл ma,
∆b = tтабл mb
Доверительные интервалы рассчитываются следующим образом:
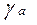 =a ± Da
=a ± Da 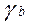 =b ± Db;
=b ± Db;
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значение.
Прогнозное значение результативного признака yp определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения xp. Вычисляется средняя стандартная ошибка прогноза
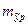 =
= 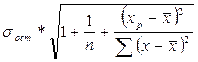 ,
,
где 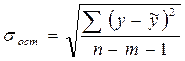 .
.
Далее строится доверительный интервал прогноза:
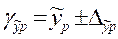 ;
;
где 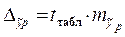
 2014-02-09
2014-02-09 1245
1245







