Логическим связкам соответствуют логические операции над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.
Логические значения результатов этих операций связаны с логическими значениями исходных высказываний. Соответствие между высказываниями определяется таблицей истинности.
1. Отрицание. Отрицанием высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно. Обозначается 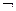 Р или
Р или 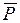 . Операции соответствует логическая связка «не». Таблица истинности имеет вид
. Операции соответствует логическая связка «не». Таблица истинности имеет вид
| P | 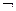 Р Р |
| И | Л |
| Л | И |
2. Конъюнкция. Конъюнкцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания. Обозначается P&Q или РÙQ. Операции соответствует логическая связка «и». Таблица истинности имеет вид
| P | Q | P&Q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
3. Дизъюнкция. Дизъюнкцией двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.Обозначается PÚQ. Операции соответствует логическая связка «или». Таблица истинности имеет вид
| P | Q | PÚQ |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
4. Импликация. Импликацией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно. Обозначается PÉQ (или Р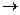 Q). Высказывание Р называется посылкой импликации, а высказывание Q – следствием. Операции соответствует логическая связка «если…,то». Таблица истинности имеет вид
Q). Высказывание Р называется посылкой импликации, а высказывание Q – следствием. Операции соответствует логическая связка «если…,то». Таблица истинности имеет вид
| P | Q | P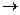 Q Q |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
5. Эквиваленция. Эквиваленцией двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают. Обозначается Р~Q, или Р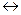 Q, или
Q, или 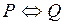 . Операции соответствует логическая связка «тогда и только тогда». Таблица истинности имеет вид
. Операции соответствует логическая связка «тогда и только тогда». Таблица истинности имеет вид
| P | Q | P~Q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
С импликацией связано постоянное упоминание математиками «необходимое условие» и «достаточное условие». В табл. 1. приведены разные виды импликаций, их запись, определение и прочтение.
Таблица 1
| Вид импликации | Обозначение | Определение | Прочтение |
| Импликация | 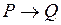 | P является достаточным условием для Q | Если имеет место P, то Q также будет иметь место |
| Конверсия импликации | 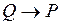 | P является необходимым условием для Q | Если имеет место Q, то P также будет иметь место |
| Двойная импликация (эквивалентность) | 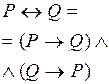 | Р является необходимым и достаточным условием для Q | Р имеет место, если и только если имеет место Q |
Наряду с основными операциями, могут использоваться дополнительные, полученные из основных через операцию «отрицание»: штрих Шеффера, стрелка Пирса, сумма по модулю два.
6. Штрих Шеффера. Штрихом Шеффера высказываний P и Q называется высказывание, ложное тогда и только тогда, когда истинны оба высказывания. Обозначается P|Q. По определению, P|Q =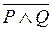 – антиконъюнкция высказываний P и Q. Таблица истинности имеет вид
– антиконъюнкция высказываний P и Q. Таблица истинности имеет вид
| P | Q | P / Q |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | Л |
7. Стрелка Пирса. Стрелкой Пирса высказываний P и Q называется высказывание, истинное тогда и только тогда, когда ложны оба высказывания. Обозначается 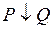 . По определению,
. По определению, 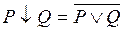 – антидизъюнкция высказываний P и Q. Таблица истинности имеет вид
– антидизъюнкция высказываний P и Q. Таблица истинности имеет вид
| P | Q | P 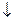 Q Q |
| И | И | Л |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
8. Сумма по модулю два. Суммой по модулю два двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинно одно из высказываний. Обозначается 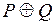 . По определению,
. По определению, 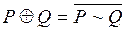 – антиэквивалентность высказываний P и Q.
– антиэквивалентность высказываний P и Q.
| P | Q | P 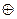 Q Q |
| И | И | Л |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
Пример. Определить значение истинности высказывания К, если высказывание 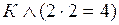 ложно.
ложно.
Решение.
Конъюнкция высказываний есть ложное высказывание в случае, когда по меньшей мере одно из входящих в конъюнкцию составляющих высказываний (членов конъюнкции) ложно. В нашем случае второе составляющее высказывание «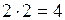 » истинно, а конъюнкция двух высказываний ложна. Поэтому К ложно.
» истинно, а конъюнкция двух высказываний ложна. Поэтому К ложно.
Пример. Сформулировать и записать в виде конъюнкции или дизъюнкции условие истинности предложения «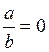 » (a,b – действительные числа).
» (a,b – действительные числа).
Решение.
Дробь равна нулю лишь в том случае, когда числитель равен нулю, а знаменатель отличен от нуля, т.е. 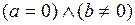 .
.
 2014-02-09
2014-02-09 2615
2615
