2014-02-09
869
Рис. 3.1. Условное графическое изображение индуктивности
Вокруг протекающего электрического тока всегда существует магнитное поле, которое характеризуют магнитной индукцией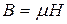 
, измеряемой в теслах (Тл).
Если проводник с током охватывает некоторую площадь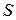 
, то с ним связывают величину собственного магнитного поля как магнитный поток, равный потоку вектора 
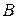через площадь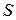
.
Магнитный поток измеряют в веберах: [Вб] = [Тл].[м2].
Положительное направление магнитного поля определяют по правилу правоходового винта, вращаемого по току. Магнитному потоку также приписывают положительное или отрицательное направление, хотя поток – скалярная величина. Вытекающий из замкнутой поверхности поток считают положительным, втекающий – отрицательным.
Рассмотрим катушку индуктивности, образованную одним витком проводника (рис. 3.2, а). Ток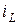 
, протекающий по проводнику, создаёт магнитное поле, величину потока которого через площадь этого витка обозначим как 
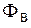и назовём собственным магнитным потоком витка.
Индуктивностью витка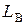 
называют отношение собственного магнитного потока к току, который создаёт этот поток, т.е.
.
Индуктивность измеряют в генри: [Гн] = [Вб]/[А] = [Тл].[м2]/[А].
Предположим, что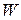 
последовательно соединённых витков образуют многовитковую катушку индуктивности. Как правило, витки катушки индуктивности располагают на минимально близком расстоянии друг от друга соосно и параллельно друг другу (рис. 3.2, б). Витки, в принципе, различны как по расположению в пространстве, так и по своей площади, но эти различия будем считать минимальными.
Ток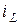 
катушки индуктивности создаёт магнитное поле, величина потока которого через один любой виток номера 
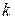этой катушки равна 
.
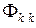Одна часть силовых линий магнитного потока витка замыкается вокруг проводника, не пересекая площади других витков катушки (малые эллипсы на рис. 3.2, б). Её называют потоком рассеяния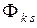 
витка номера 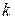. Вторая часть магнитного потока этого витка пересекает площади других витков. Её называют потоком взаимоиндукции витка 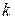с витком 
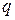и обозначают как 
.
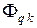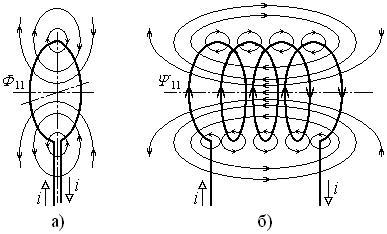
Рис. 3.2. Одновитковая (а) и многовитковая (б) катушки индуктивности
Потокосцеплением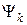 
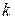витка называют магнитный поток равный сумме магнитных потоков, пересекающих площадь данного витка и образованных всеми витками катушки индуктивности:
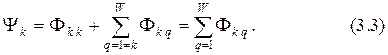
Здесь первое слагаемое – поток самоиндукции витка 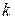, второе слагаемое – поток взаимоиндукции витка 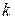со всеми остальными витками катушки индуктивности, первый индекс – номер рассматриваемого витка, второй – номер витка, создающего магнитный поток в рассматриваемом витке.
Полный магнитный поток катушки индуктивности является алгебраической суммой потоков всех её витков. Этот магнитный поток называют потокосцеплением самоиндукции
Индуктивностью катушки называют отношение потокосцепления самоиндукции к току
Отсюда получаем выражение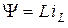 
.
Теоретически все витки считают абсолютно одинаковыми, а потоки рассеивания равными нулю. Поэтому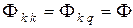 
и формулы (3.3) и (3.4) преобразуются к виду
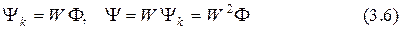
соответственно.
Из формул (3.5) и (3.6) следует, что
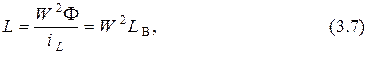
то есть индуктивность катушки индуктивности пропорциональна квадрату числа витков.
Связь между током и электродвижущей силой (эдс) самоиндукции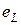 
, называемой иногда наведённой эдс, устанавливается в соответствии с законом электромагнитной индукции
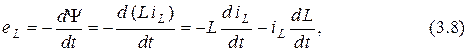
или при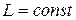 
Напряжением называют величину, противоположную эдс, то есть
Из уравнения (3.9) следует, что возникающая эдс препятствует изменению тока в индуктивности, то есть при увеличении тока, когда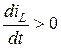 
, возникает отрицательная эдс. Знак же напряжения на индуктивности совпадает со знаком производной тока по времени.
Уравнение (3.10) представляет собой дифференциальную форму закона Ома. Размерность индуктивности в соответствии с этим выражением можно представить в виде [Гн] = [В] [с]/[А] = [Ом] [с].
Из уравнения (3.10) получаем выражение
которое является выражением закона Ома в интегральной форме.
Отсюда следует, что ток в индуктивности скачком меняться не может, т.к. для его изменения требуется время. А напряжение на выводах индуктивности может изменяться скачком.
Отношение напряжения к току согласно закону Ома есть величина электрического сопротивления элемента. Поэтому выражение
представляет собой дифференциальную, а выражение
– интегральную форму величины сопротивления индуктивности переменному току.
Согласно выражениям (1.7) и (3.10) энергия, запасённая в магнитном поле индуктивного элемента за промежуток времени от 0 до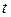 
с учётом того, что 
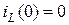, может быть рассчитана по формуле
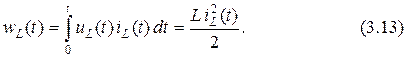
Мощность есть скорость изменения энергии и для индуктивности она равна
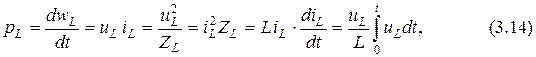
где, как и ранее, для краткости обозначено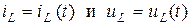 
.
Мощность магнитного поля в зависимости от знака производной может быть как положительной, так и отрицательной. Положительная мощность означает, что ток через индуктивность возрастает, магнитный поток увеличивается, то есть происходит накопление магнитной энергии, поступающей от источника энергии в индуктивность. Отрицательная мощность означает, что индуктивность возвращает (отдаёт) накопленную энергию магнитного поля обратно в электрическую цепь.
