2014-02-09
1156
Мкость
Рис. 2.3. Дифференциальное сопротивление с отрицательным участком
Сопротивления являются пассивными элементами цепи, так как они только потребляют энергию из электрической цепи. Мощность, выделяемая в виде тепла в резистивном элементе в момент времени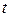 
, выражается законом Джоуля-Ленца.
С учётом соотношений (1.8) и (2.1) получаем
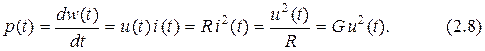
Так как величины сопротивления и проводимости положительны, а мощность является квадратичной функцией тока или напряжения, то в резисторе она не может быть отрицательной. Следовательно, энергия всегда поступает от источника энергии в сопротивление и рассеивается в нём в виде тепла.
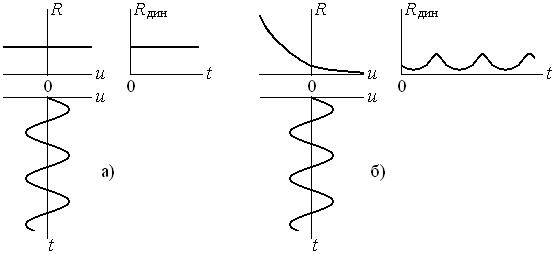
Рис. 2.4. Динамические сопротивления линейного (а) и нелинейного (б) элементов
Ёмкостью называют такой идеализированный элемент электрической цепи, в котором происходит только накопление энергии электрического поля. Потери и накопление энергии в виде магнитного поля отсутствуют или пренебрежимо малы.
Ёмкость заменяет собой конструктивный элемент, называемый конденсатором. Ёмкость характеризует свойство любого тела накапливать заряды в электрическом поле и количественно может быть описана формулой
Ёмкость измеряют в фарадах: [Ф] = [Кл]/[В]. При этом всегда заряд и напряжение имеют одинаковый знак, так что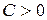 
. Если зависимость заряда от напряжения линейна, то ёмкость постоянна. В противном случае ёмкость нелинейна. Условное графическое изображение ёмкости представлено на рис. 2.5 и напоминает обкладки плоского конденсатора.
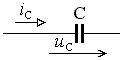
Рис. 2.5. Условное графическое изображение ёмкости
Используя формулу (2.9) с учётом (1.4) находим уравнение тока, протекающего через ёмкость
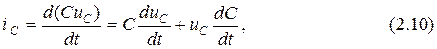
которое при C = const упрощается до
Из выражений (2.10) и (2.11) следует, что размерность ёмкости можно представить как [Ф] = [с]/[Ом].
Так как из формулы (1.4) можно получить уравнение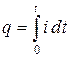 
, то
Следовательно, напряжение на конденсаторе мгновенно (скачком) изменяться не может, потому что требуется время для накопления заряда.
В то же время ток, протекающий через ёмкость, может изменяться скачком. Он положителен, когда возрастает заряд или когда возрастает напряжение.
Для случая, когда 
, выражения (2.11) и (2.12) представляют собой дифференциальную и интегральную формы закона Ома соответственно.
Отношение напряжения к току согласно закону Ома есть величина электрического сопротивления элемента. Поэтому выражение
представляет собой дифференциальную, а выражение
– интегральную форму записи величины сопротивления ёмкости.
По определению (1.6) энергия электрического поля в произвольный момент времени 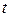с учётом того, что 
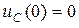, может быть вычислена по формуле
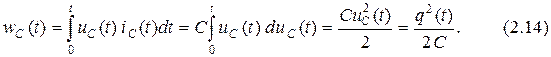
Мощность есть скорость изменения энергии и для ёмкости она равна
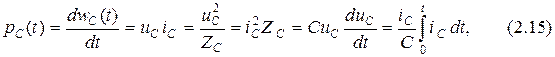
где для краткости приняты обозначения: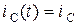 
и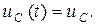 
Когда имеет место накопление заряда, то напряжение между обкладками конденсатора возрастает по модулю, знаки производной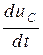 
и напряжения U c совпадают и мощность положительна. А это означает, что в ёмкость поступает электрическая энергия из внешней цепи. Если заряд убывает, то меняется знак производной и мощность становится отрицательной, что свидетельствует о возвращении во внешнюю цепь ранее накопленной в ёмкости энергии.
