2014-02-09
525
Алгоритм решения поставленной задачи начинается с ввода исходных данных (рис. 4.4, символ 1).
Вначале вводят требуемые параметры выпрямителя: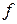 
, 
, 
, 
, 
, 
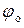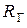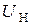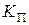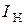и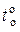 
.
Затем вводят параметры диода: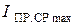 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
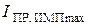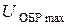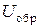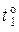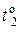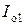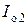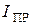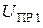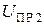Вводят дополнительные данные для расчёта: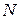 
− количество расчётных точек за период гармонического сигнала (для получения достаточно высокой точности следует выбирать число точек из условия 
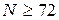), М − количество периодов, 
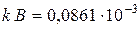эВ / град – постоянную Больцмана, 
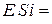= 1,12 эВ – ширину запрещённой зоны для кремния, 
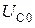− начальное напряжение на ёмкости, относительную погрешность нахождения выходного напряжения (например, 
).
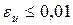3. Расчёт начальных значений величин (рис. 4.4, символ 2)
Рассчитывают:
1) 
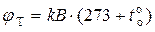− температурный потенциал,
2) 
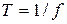– период эдс,
3) 
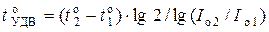− температуру удвоения обратного тока p-n -перехода,
4) 
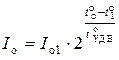− обратный ток p-n -перехода при температуре ,
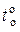5) 
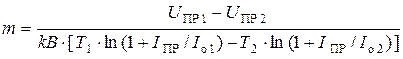− коэффициент неидеальности обеднённого слоя,
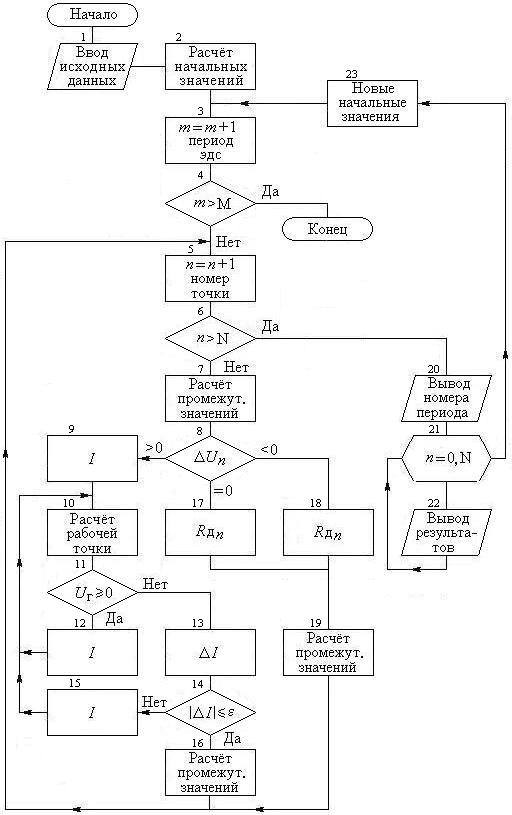
Рис. 4.4. Схема алгоритма расчёта выпрямителя, работающего на ёмкостную нагрузку
6) 
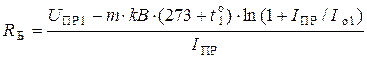− базовое сопротивление диода,
7) 
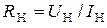− сопротивление нагрузки,
8) 
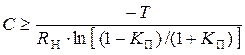− ёмкость выпрямителя,
9) 
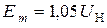− амплитуду эдс (первое приближение),
10) 
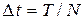− шаг по времени,
11) 
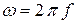− угловую частоту эдс,
12) 
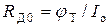− эквивалентное сопротивление диода при нулевых начальных условиях,
13) 
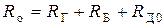− начальная величина суммарного сопротивления,
14) 
− начальное значение постоянной времени контура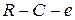 
,
15) 
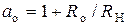− начальное значение коэффициента 
,
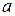16) 
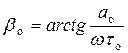− начальное значение 
,
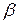17) 
, 
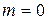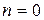− начальные значения счётчиков номера цикла и номеров точек.
4. Начало цикла расчётов и проверка достижения окончания расчётов (рис. 4.4, символы 3 и 4)
5. Начало цикла расчётов переходного процесса и проверка достижения окончания расчёта точек в пределах одного периода (рис. 4.4, символы 5 и 6)
6. Расчёт промежуточных значений электрических величин (рис. 4.4, символ 7)
Рассчитывают:
1) 
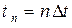− время в текущей точке,
2) 
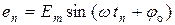− эдс в текущей точке,
3) 
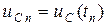− выходное напряжение в текущей точке по формуле (4.16),
4) 
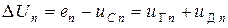− разность напряжений, равная сумме напряжений на внутреннем сопротивлении источника эдс и диоде в текущей точке.
