2014-02-09
621
Система функций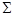 
называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой 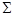(является суперпозицией функций этой системы).
Из теоремы 1 (из предыдущей лекции) следует, что система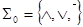 
является функционально полной. Равным образом, функционально полна любая система 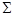, через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание. Действительно, для любой логической функции 
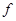из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 1 (из предыдущей лекции)) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы 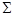. Аналогично обосновывается более общее утверждение.
Теорема 1. Если все функции функционально полной системы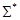 
представимы формулами над системой 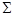, то система 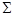также функционально полна.
