2014-02-09
548
Составить полиномы Жегалкина для данных функций:
а)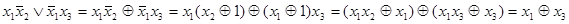 
,
б)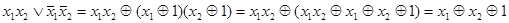 
.
Заметим, что если в полученных полиномах Жегалкина произвести обратную замену функций, то получим упрощённые формулы булевой алгебры.
Теорема 2. Для всякой логической функции существует полином Жегалкина и притом единственный.
Существование такого полинома, по сути, уже доказано, а для доказательства его единственности достаточно показать существование взаимно однозначного соответствия между множеством всех функций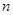 
переменных и множеством всех полиномов Жегалкина.
Функция, у которой полином Жегалкина имеет вид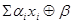 
, где параметры 
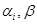равны нулю или единице, называется линейной.
Все функции от одной переменной линейны. Также линейными являются функции эквивалентность и сумма по модулю 2.
