Применим процедуру из теоремы о детерминизации к НКА N1 из примера 1 (рис. 5.16).
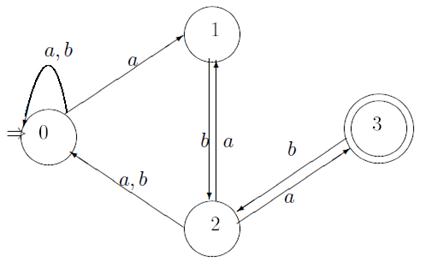
Рис. 5.16. Диаграмма НКА
Заметим, что состояние 4 исчезло, так как в автомате N1 в него можно было попасть только по ε -переходу.
На втором этапе детерминизируем M1. ДКА A будет иметь 16 состояний:
QA= {∅, {0}, {1}, {2}, {3}, {0, 1}, {0, 2}, {0, 3}, {1, 2}, {1, 3}, {2, 3}, {0, 1, 2}, {0, 1, 3}, {0, 2, 3}, {1, 2, 3}, {0, 1, 2, 3}}.
Во множество заключительных состояний войдут состояния, содержащие заключительное состояние 3 автомата M1:
FA= {{3}, {0, 3}, {1, 3}, {0, 1, 3}, {0, 2, 3}, {1, 2, 3}, {0, 1, 2, 3}}.
Функция переходов ΦA определена в следующей таблице
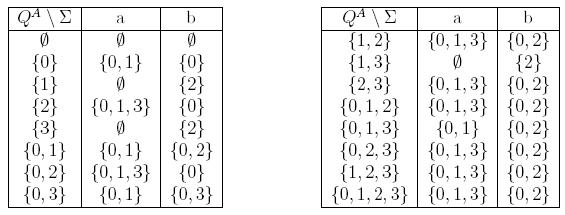
На самом деле нас интересуют лишь те состояния, в которые можно попасть из начального состояния {0}. Несложный анализ показывает, что их только три: {0, 1}, {0, 2} и {0, 1, 3}. Остальные состояния не достижимы из {0} и, следовательно, не влияют на работу автомата A. Их можно отбросить. Таким образом, в диаграмме автомата остаются 4 состояния, показанные на рис. 5.17.
Замечание. В рассмотренном примере у построенного ДКА A оказалось не больше состояний, чем у исходного НКА N1. К сожалению, это не всегда так. Существуют примеры НКА с n состояниями, для которых эквивалентные ДКА содержат не менее 2n состояний.
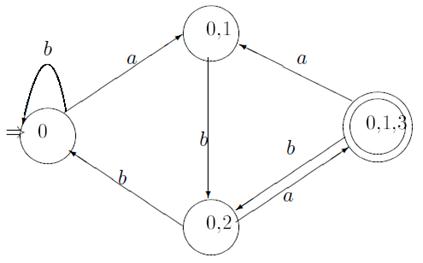
Рис. 5.17. Диаграмма ДКА
 2014-02-09
2014-02-09 543
543








