Алгоритм Хаффмана. Данные для электронной обработки представляют собой некоторую последовательность чисел

Данные для электронной обработки представляют собой некоторую последовательность чисел. Обычно каждое число в этой последовательности представляется битовой цепочкой фиксированной длины. Например, если рассматривать данные как последовательность байтов (8 битных кусочков), то битовая цепочка 0000000b = 0, 0000001b = 1, 11111111b = 255 и т.д.

Идея алгоритма Хаффмана заключается в следующем. Если некоторые данные содержат различные числа, представленные в виде битовых цепочек фиксированной длины и частоты, с которыми различные числа присутствуют в этих данных, существенно различаются, то заменив битовые цепочки фиксированной длины на битовые цепочки различной длины, причем так, чтобы более часто встречающимся числам соответствовали бы более короткие цепочки, можно получить уменьшение объема данных.

Далее будем предполагать данные в виде последовательности байт (8 битных кусочков), хотя это необязательно, и можно применять алгоритм Хаффмана к битовым цепочкам любой фиксированной длины.

Рассмотрим пример: имеем данные длиной в 100 байт, включающие шесть различных чисел: 1, 2, 3, 4, 5, 7. Сжимая данные по алгоритму Хаффмана, первое, что необходимо сделать – это подсчитать сколько раз встречается каждое число в данных. После подсчета частоты вхождения каждого числа мы получаем таблицу частот. Таблица имеет ненулевые значения частот для чисел 1, 2, 3, 4, 5, 7. Числа с нулевой частотой далее не участвуют в алгоритме, о них можно просто забыть. Ячейки таблицы будем называть «узлами».

Полная частотная таблица метода Хаффмана:

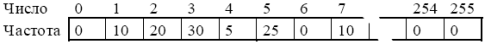
Ненулевая часть частотной таблицы:

Найдем в таблице наименьшие частоты. Для этого удобно отсортировать таблицу по возрастанию. В нашем случае это 5 и 10. Сформируем из узлов 5 и 10 новый узел, частота вхождения для которого будет равна сумме частот. Сами узлы, образовавшие новый узел, более не участвуют в создании новых узлов.

Отсортированная таблица:

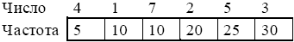
Новый узел таблицы:

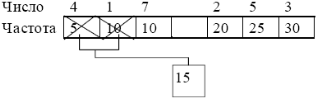
Новый узел и оставшиеся узлы таблицы частот образуют новую таблицу, для которой повторяют операцию добавления узла. Опять самая низкая частота 10 (узел для числа 7) и 15 (новый узел). Снова добавляем узел.

Формирование второго узла в методе Хаффмана:

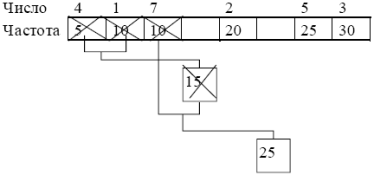
Продолжаем добавлять узлы, пока не останется единственный узел (корень). Структура, где каждый нижележащий узел имеет связь с двумя вышележащими узлами, носит название «двоичное дерево» (далее просто дерево).

Дерево узлов в методе Хаффмана:

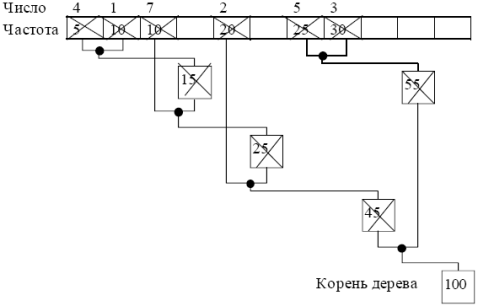
Теперь, когда дерево создано, можно вычислить коды (битовые цепочки для кодирования исходных чисел) и закодировать данные. Вычисление кода числа начинается от корня дерева. Для вычисления кода, необходимо, двигаясь по дереву от корня к числу в исходной таблице, подсчитать число пройденных узлов. Это значение будет равно длине битовой цепочки кода. И проследить для каждого узла повороты: если поворот в узле осуществляется налево, то в цепочке битов устанавливается значение 0, если направо — 1.

Например, для числа 3 от корня до исходного узла пройдем два узла, т.е. длина кода два бита. Первый от корня поворот направо 1 и второй, тоже направо 1. Тогда код Хаффмана для числа равен 11b. Выполнив вычисление для всех чисел, получим следующие коды Хаффмана:

1. → 0111b (4 бита);

2. → 00b (2 бита);

3. → 11b (2 бита);

4. → 0110b (4 бита);

5. → 10b (2 бита);

7. → 010b (3 бита).

Каждый символ изначально представлялся 8-ю битами, и так как мы уменьшили число битов, необходимых для представления каждого символа, мы, следовательно, уменьшили размер выходного файла. Результирующее сжатие может быть вычислено следующим образом, см. табл. 1. Первоначальный размер данных: 100 байт или 800 бит; размер сжатых данных: 30 байт или 240 бит; так что получили размер данных 0.3 от исходного.

Таблица 1 – Вычисление степени сжатия данных.

Число	Частота	Исходный размер, бит	Уплотненный размер, бит	Уменьшение размера, бит
1.
2.
3.
4.
5.
7.
ВСЕГО

Заметим, что в той же пропорции будет уменьшен размер данных для более длинной порции данных, если относительные частотные характеристики не изменятся.

Следует помнить, что для восстановления первоначальных данных, необходимо иметь декодирующее дерево. Следовательно, необходимо сохранить дерево вместе с данными. В итоге это приводит к увеличению размеров сжатых данных.

Если для ссылки на узлы использовать номер узла в массиве узлов, то такой номер может изменяться от 0 до 511 (для байта), т.е. для хранения ссылки необходимо 9 бит. В рассмотренном примере дерево состоит из 5 узлов по две ссылки — 18 бит, итого 90 бит необходимо для сохранения информации по дереву.

Правильный подсчет степени сжатия: первоначальный размер данных: 100 байт или 800 бит; размер сжатых данных: 240 бит и 90 бит данных о дереве — так что в результате получили размер данных 0.41 исходного.

Метод Хаффмана не всегда способен уменьшить размер данных. Очевидно, что для данных, где встречаются все числа (0÷255) и частоты их равны, получится длина кода для каждого числа 8 бит и никакого сжатия нет. Можно придумать и другие сочетания, приводящие к аналогичному результату. Следует заметить, что невозможность сжать данные по алгоритму Хаффмана не означает отсутствие возможности сжатия вообще. Например, очевидно, что любая последовательность, где встречаются все числа (0÷255) с равными частотами несжимаема по Хаффману. Но, если числа в данных расположены группами, состоящими из одинаковых чисел (1,1,1,1,7,7,7,7 и т.д.), то такие данные легко сжать методом Running. Вопрос о степени избыточности информации в произвольных данных в общем случае не решен.