Минимизация сложных высказываний.
Существует несколько способов минимизации сложных высказываний. Рассмотрим самые распространенные:
· метод Квайна;
· карты Вейча;
· минимизирующие карты.
Алгоритм метода Квайна включает в себя следующие этапы:
1. Любая формула  приводится к СДНФ.
приводится к СДНФ.
2. СДНФ приводится к сокращенной ДНФ (СкДНФ). При получении СкДНФ используются следующие формулы равносильности:
а) Формула склеивания
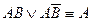
б) Формула неполного склеивания
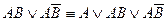
в) Формула поглощения
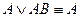
Применяя все возможные процедуры склеивания, СДНФ приводится к СкДНФ.
3. Минимальная форма формулы  (МДНФ
(МДНФ  ) получается на основе импликантной матрицы путем нахождения минимального покрытия этой матрицы. Импликанта – это элементарная конъюнкция СкДНФ. Конституента единицы – это элементарная конъюнкция СДНФ. Импликантная матрица – это матрица импликант и констиуент единиц. (столбцы - конституенты единицы, строки – импликанты). МДНФ может быть несколько.
) получается на основе импликантной матрицы путем нахождения минимального покрытия этой матрицы. Импликанта – это элементарная конъюнкция СкДНФ. Конституента единицы – это элементарная конъюнкция СДНФ. Импликантная матрица – это матрица импликант и констиуент единиц. (столбцы - конституенты единицы, строки – импликанты). МДНФ может быть несколько.
ПРИМЕР.
Необходимо найти МДНФ формулы:
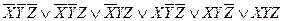
1 2 3 4 5 6
Осуществляем всевозможные склеивания
|
|
|
1-2 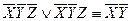
1-4 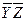
2-3 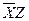
3-6 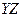
4-5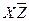
5-6 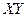
СкДНФ имеет вид:
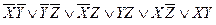
Составляем импликантную матрицу
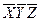 | 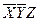 | 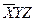 | 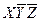 | 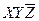 | 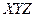 | |
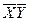 | + | + | ||||
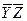 | + | + | ||||
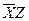 | + | + | ||||
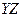 | + | + | ||||
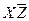 | + | + | ||||
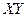 | + | + |
По данной импликантной матрице можно выбрать следующие МДНФ
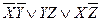
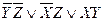
 2014-02-09
2014-02-09 1749
1749








