2014-02-09
1190
Литерой - называется элемент высказывания x или её отрицание.
Элементарной дизъюнкцией называется выражение следующего вида:
, (2.2)
где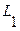 
- литера.
Элементарной конъюнкцией называется выражение следующего вида:
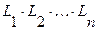, (2.3)
Дизъюнктивной нормальной формой (ДНФ) формулы 
называется выражение вида:
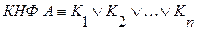, (2.4)
где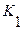 
- элементарная конъюнкция.
Конъюнктивной нормальной формой (КНФ) формулы называется выражение вида:
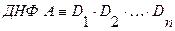, (2.5)
где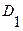 
- элементарная дизъюнкция.
Любую формулу можно представить в виде ДНФ или КНФ.
ПРИМЕР
Пусть дана формула
Требуется получить ДНФ и КНФ данной формулы.
Применяя формулы равносильности, получаем КНФ :
Применяя формулы равносильности, получаем ДНФ :
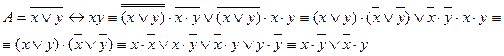
Совершеннойдизъюнктивной нормальной формой(СДНФ) формулы называется такая ДНФ, для которой выполняются следующие условия:
1. Все элементарные конъюнкции, входящие в ДНФ , различны.
2. Все элементарные конъюнкции, входящие в ДНФ , содержат литеры, соответствующие всем переменным.
3. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит двух одинаковых литер.
4. Каждая элементарная конъюнкция, входящая в ДНФ , не содержит переменную и ее отрицание.
СДНФ можно получить двумя способами:
1. по таблице истинности;
2. с помощью равносильных преобразований.
Первый способ получения СДНФ рассмотрен выше. Рассмотрим второй способ, который состоит в следующем:
С помощью равносильных преобразований формулы получают ДНФ . При этом в полученной ДНФ возможны следующие ситуации:
1. Элементарная конъюнкция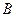 
ДНФ не содержит переменную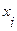 
, тогда используются следующие равносильные преобразования:
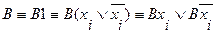
2. Если в ДНФ входят две одинаковые элементарные конъюнкции, то используя следующее равносильное преобразование:
,
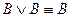одну элементарную конъюнкцию можно отбросить.
3. Если элементарная конъюнкция 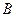ДНФ содержит одновременно переменную 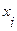и ее отрицание, то используя следующие равносильные преобразования:
,
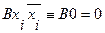эту элементарную конъюнкцию можно отбросить
4. Если элементарная конъюнкция 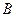ДНФ содержит дважды переменную 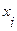, то используя следующее равносильное преобразование:
,
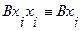одну переменную 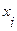можно отбросить
СДНФ формулы существует в единственном виде.
ПРИМЕР
Получить СДНФ формулы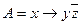 
С помощью равносильных преобразований получаем СДНФ :
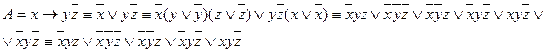
С помощью таблицы истинности получаем СДНФ :
 |  |  |  |  | |
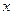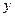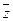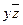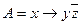СДНФ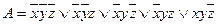 
Очевидно, что в результат двух способов совпадает.
Совершеннойконъюнктивной нормальной формой(СКНФ) формулы называется такая КНФ, для которой выполняются следующие условия:
1. Все элементарные дизъюнкции, входящие в КНФ , различны.
2. Все элементарные дизъюнкции, входящие в КНФ , содержат литеры, соответствующие всем переменным.
3. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит двух одинаковых литер.
4. Каждая элементарная дизъюнкция, входящая в КНФ , не содержит переменную и ее отрицание.
СКНФ можно получить двумя способами:
1. по таблице истинности;
2. с помощью равносильных преобразований.
По первому способу по таблице истинности получаем СДНФ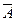 
, а СКНФ можно получить, следуя следующему правилу
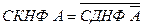
С помощью равносильных преобразований формулы получают КНФ . При этом в полученной КНФ возможны следующие ситуации:
1. Элементарная дизъюнкция 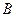КНФ не содержит переменную 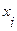, тогда используются следующие равносильные преобразования:
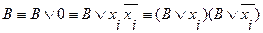
2. Если в КНФ входят две одинаковые элементарные дизъюнкции, то используя следующее равносильное преобразование:
,
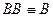одну элементарную дизъюнкцию можно отбросить.
3. Если элементарная дизъюнкция 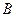КНФ содержит одновременно переменную 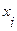и ее отрицание, то используя следующие равносильные преобразования:
,
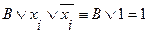эту элементарную дизъюнкцию можно отбросить.
4. Если элементарная дизъюнкция 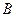КНФ содержит дважды переменную 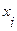, то используя следующее равносильное преобразование:
,
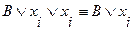одну переменную 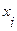можно отбросить.
СКНФ формулы существует в единственном виде.
ПРИМЕР
Получить СКНФ формулы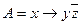
С помощью равносильных преобразований получаем СКНФ :
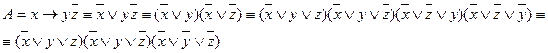
С помощью таблицы истинности получаем СДНФ :
| | | | | | | |
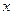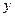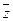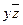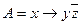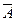СДНФ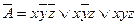 
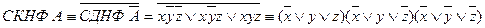
Очевидно, что в результат двух способов совпадает.
СДНФ формулы можно получить из СКНФ , используя следующее правило:
