Для предикатов кроме логических операций применимы кванторные операции: всеобщности и существования.
Пусть 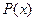 - предикат, определенный на множестве
- предикат, определенный на множестве 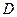 . Тогда
. Тогда 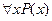 - означает «для всякого (любого)
- означает «для всякого (любого) 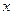 истинно
истинно 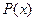 ». Символ
». Символ 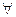 называется квантором всеобщности.
называется квантором всеобщности.
Переменную 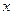 в предикате
в предикате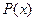 называют свободной (ей можно придавать различные значения из М), в высказывании
называют свободной (ей можно придавать различные значения из М), в высказывании 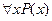 переменную
переменную 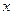 называют связанной квантором всеобщности.
называют связанной квантором всеобщности.
Пусть 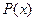 - предикат, определенный на множестве
- предикат, определенный на множестве 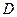 . Тогда
. Тогда 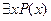 - означает «существует
- означает «существует 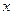 , для которого истинно
, для которого истинно 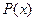 ». Символ
». Символ 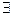 называется квантором существования.
называется квантором существования.
ПРИМЕР
Пусть на множестве натуральных чисел задан предикат 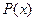 -«число
-«число 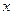 кратно 3». Используя кванторы, из данного предиката можно получить высказывания:
кратно 3». Используя кванторы, из данного предиката можно получить высказывания:
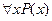 - «все натуральные числа кратны 3»;
- «все натуральные числа кратны 3»;
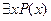 - «существуют натуральные числа, кратные 3».
- «существуют натуральные числа, кратные 3».
Очевидно, что первое из данных высказываний ложно, а второе – истинно.
Кванторные операции применяются и к многоместным предикатам. Пусть на множестве 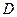 задан двухместный предикат
задан двухместный предикат 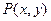 . К данному предикату могут применяться кванторные операции как по одной, так и по двум переменным.
. К данному предикату могут применяться кванторные операции как по одной, так и по двум переменным.
ПРИМЕР
Пусть предикат 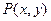 означает
означает 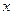 делится на
делится на 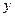 без остатка., причем обе переменные определены на множестве натуральных чисел. Тогда применение кванторных операций приводит к следующим высказываниям:
без остатка., причем обе переменные определены на множестве натуральных чисел. Тогда применение кванторных операций приводит к следующим высказываниям:
1. 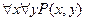 - «для любого
- «для любого 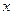 и для любого
и для любого 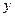 справедливо, что
справедливо, что 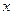 делится на
делится на 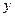 без остатка.
без остатка.
2. 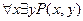 - «для любого
- «для любого 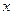 существует
существует 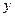 , который является делителем
, который является делителем 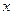 без остатка.
без остатка.
Нетрудно заметить, что первое высказывание является ложным, а второе – истинным.
Для многоместных предикатов, связанных по одной переменной справедливы следующие формулы:
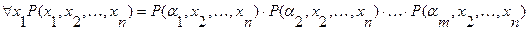 ,
,
где 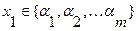
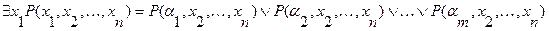 ,
,
где 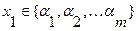
 2014-02-09
2014-02-09 1123
1123








