Две формулы логики предикатов  и
и 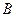 называются равносильными на области
называются равносильными на области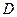 , если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области
, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области 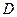 .
.
Две формулы логики предикатов  и
и 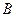 называются равносильными, если они равносильны во всякой области.
называются равносильными, если они равносильны во всякой области.
Очевидно, что все формулы равносильности алгебры высказываний будут верны, если в них вместо переменных подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов:
Закон де Моргана:
1. 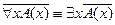
2. 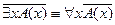
3. 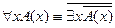
4. 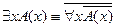
5. 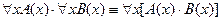
6. 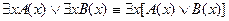
7. 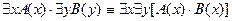
Для произвольного высказывания 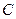 (предиката, не связанного по переменной
(предиката, не связанного по переменной 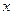 ) справедливы следующие формулы равносильности:
) справедливы следующие формулы равносильности:
8. 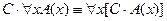
9. 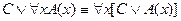
10. 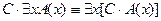
11. 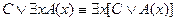
12. 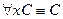
13. 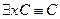
Формулы замены переменных (где 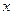 и
и 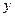 из одной предметной области):
из одной предметной области):
14. 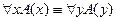
15. 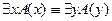
 Предваренная нормальная форма предиката
Предваренная нормальная форма предиката
Формула предиката имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции, и кванторные операции, а операция отрицания отнесена к элементарному предикату.
ПРИМЕР
Пусть дан предикат 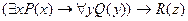 . Привести данный предикат к нормальной форме
. Привести данный предикат к нормальной форме
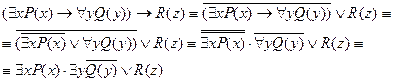
Предварённой нормальной формой предиката называется такая нормальная форма предиката, в которой кванторные операторы либо отсутствуют, либо используются после операций алгебры логики.
ПРИМЕР
Привести предикат из предыдущего примера к предваренной нормальной форме предиката
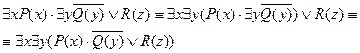
 2014-02-09
2014-02-09 3755
3755
