Пусть необходимо найти минимальный путь из вершины 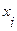 в вершину
в вершину 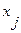 .
.
1. Выписываются все вершины с 1 по n. Вершина  помечается индексом 0.
помечается индексом 0.
2. Находится первый фронт волны 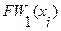 как множество вершин образа вершины
как множество вершин образа вершины 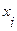 .
.
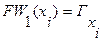 (3.17)
(3.17)
3. Все вершины, принадлежащие первому фронту волны, помечаются индексом 1.
4. Вводится счетчик шагов (фронтов волны) 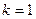 .
.
5. Если 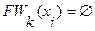 или
или 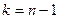 , то вершина
, то вершина 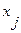 недостижима из вершины, и работа алгоритма на этом заканчивается. В противном смысле переходим к пункту 6.
недостижима из вершины, и работа алгоритма на этом заканчивается. В противном смысле переходим к пункту 6.
6. Если 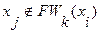 , то переходим к пункту 8. В противном случае существует путь из вершины
, то переходим к пункту 8. В противном случае существует путь из вершины 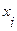 в вершину
в вершину 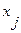 длиной в
длиной в 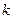 единиц, и этот путь минимальный:
единиц, и этот путь минимальный:
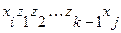
7. Находятся промежуточные вершины 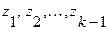 z по правилу:
z по правилу:

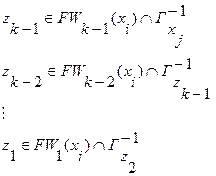 , (3.18)
, (3.18)
где 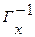 - прообраз вершины
- прообраз вершины 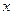 - множество вершин, из которых заходят дуги в вершину
- множество вершин, из которых заходят дуги в вершину 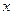
8. Определяется 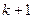 фронт волны как все непомеченные вершины, принадлежащие образу вершин
фронт волны как все непомеченные вершины, принадлежащие образу вершин 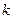 - го фронта волны. Помечаются индексом
- го фронта волны. Помечаются индексом 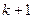 вершины
вершины 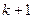 фронта волны. Далее осуществляется переход к пункту 5.
фронта волны. Далее осуществляется переход к пункту 5.
ПРИМЕР
Пусть задан граф матрицей смежности:
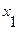 | 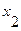 | 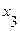 | 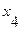 | 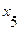 | 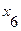 | |
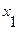 | ||||||
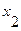 | ||||||
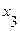 | ||||||
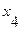 | ||||||
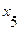 | ||||||
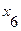 |
Необходимо найти минимальный путь из вершины 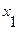 в вершину
в вершину 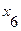 (по алгоритму «фронта волны»).
(по алгоритму «фронта волны»).
1. Выпишем все вершины. Вершина 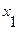 помечается индексом «0»
помечается индексом «0»
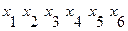
2. Находится первый фронт волны:
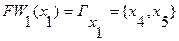
3. Все вершины, принадлежащие первому фронту волны, помечаются индексом «1».
0 1 1
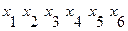
4. Так как 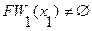 ,
, 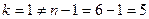 и
и 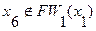 , то определяем второй фронт волны:
, то определяем второй фронт волны:
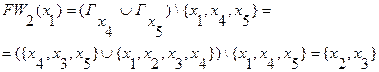
5. Все вершины, принадлежащие второму фронту волны, помечаются индексом «2».
0 2 2 1 1
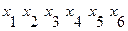
6. Так как 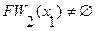 ,
, 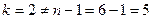 и
и 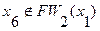 , то определяем третий фронт волны:
, то определяем третий фронт волны:
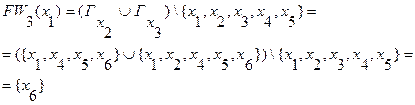
7. Так как 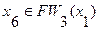 , то существует путь из вершины
, то существует путь из вершины 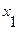 в вершину
в вершину 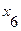 длиной 3 единицы:
длиной 3 единицы:
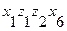
8. Находятся промежуточные вершины 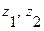 :
:
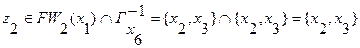
Выберем 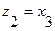
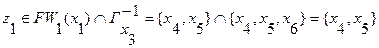
Выберем 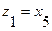
Таким образом, минимальный путь из вершины 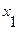 в вершину
в вершину 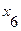 имеет вид:
имеет вид:
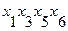
 2014-02-09
2014-02-09 6387
6387
