Cx = Fx/x = Cx растяж+ C изгиб
Жесткость на растяжение:
для 3 имеем z/l = Fz/E*S; E - модуль упругости; S – сечение.
 S =π*D2/4 S = a*b
S =π*D2/4 S = a*b
Cz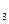 =Fz/z =2*E*S/l
=Fz/z =2*E*S/l
Cx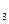 =Cy
=Cy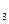
Fx = Tупр;
Tупр = 2*T0*sin(a) ≈2*T0*a =
=2*T0*sin(arct(x/l)) ≈2*T0*x/l=Fx
Cизг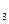 = Fx/x =2*T0/l
= Fx/x =2*T0/l
Cz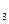 >>Cизг x,y
>>Cизг x,y
Cz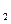 =2*E*S/l + 2*T0/l =Cy
=2*E*S/l + 2*T0/l =Cy
Cx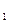 =Cy
=Cy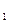 =Cz
=Cz =2*E*S/l + 4*T0/l
=2*E*S/l + 4*T0/l
 |
F = m*ax; T =T0+m*ax;
F = 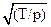 /2*l =(
/2*l =(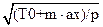 )/2*l
)/2*l
p[кг/м] – масса единицы длины.
Δf = f - f0 = Δf(m*ax)
U = Um*sin(ωt); ω = ω0+ Δω; ω =2*π*f
 |
 |
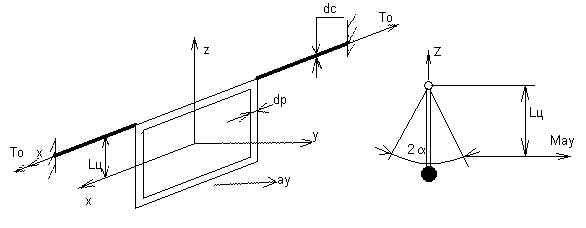
Представлен маятниково-струнный подвес, рабочим движением которого является угол закрутки торсионов 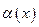 .
.
Как обеспечить Сa=min
Cb=Cγ>>Cα | è Cx,Cy,Cz
 |
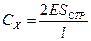
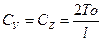 Отсюда получаем
Отсюда получаем
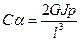 - торсионная жесткость (жесткость на кручение)
- торсионная жесткость (жесткость на кручение) 
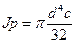 -статический полярный момент инерции сечения струны
-статический полярный момент инерции сечения струны
Ca<<Cb=Cg Cx>>Cy=Cz=f(To)
G- модуль упругости второго рода.
 2014-02-09
2014-02-09 649
649








