Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:
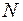 ‑ множество натуральных чисел;
‑ множество натуральных чисел;
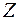 ‑ множество целых чисел;
‑ множество целых чисел;
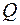 – множество рациональных или дробных чисел;
– множество рациональных или дробных чисел;
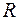 ‑ множество действительных чисел.
‑ множество действительных чисел.
Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.
Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом
Некоторое непустое подмножество  множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число
множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число 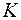 такое, что
такое, что 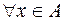 выполняется неравенство
выполняется неравенство 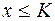 (
(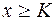 ).
).
Всякое число 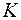 с указанным свойством называют верхней (нижней) гранью множества
с указанным свойством называют верхней (нижней) гранью множества  .
.
Непустое подмножество множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.
множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.
В противоположность этому определению, множество  называется неограниченным сверху (снизу), если какое бы число
называется неограниченным сверху (снизу), если какое бы число 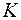 мы бы не предложили в качестве верхней (нижней) границы множества
мы бы не предложили в качестве верхней (нижней) границы множества  , всегда найдется элемент этого множества, который будет больше (меньше)
, всегда найдется элемент этого множества, который будет больше (меньше) 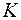 .
.
Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.
Наименьшую из верхних граней непустого подмножества множества действительных чисел  называют точной верхней гранью этого множества и обозначают sup
называют точной верхней гранью этого множества и обозначают sup  . Наибольшую из нижних граней непустого подмножества множества действительных чисел
. Наибольшую из нижних граней непустого подмножества множества действительных чисел  называют точной нижней гранью этого множества и обозначают inf
называют точной нижней гранью этого множества и обозначают inf  . Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).
. Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).
Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.
Граничной точкой множества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.
Граница множества – совокупность граничных точек множества.
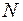 (множество натуральных чисел) ограниченно снизу (например, числом
(множество натуральных чисел) ограниченно снизу (например, числом 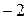 ) и не ограничено сверху;
) и не ограничено сверху;
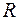 (множество действительных чисел) неограничено;
(множество действительных чисел) неограничено;
множество отрицательных чисел неограничено снизу и ограничено сверху.
Соединения. Бином Ньютона.
Рассмотрим совокупность  различных элементов
различных элементов 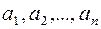 . Произвольная упорядоченная выборка из этих элементов
. Произвольная упорядоченная выборка из этих элементов
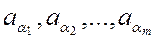 (
(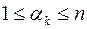 ;
; 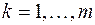 )
)
называется соединением. Эта выборка может быть как без повторений, так и с повторениями.
Раздел элементарной математики, в котором для конечных множеств рассматриваются различные соединения элементов, такие, как сочетания, размещения, перестановки, а также все виды соединений с повторениями называется комбинаторика. Задачи комбинаторики впервые рассматривались в связи с возникновением теории вероятностей, где к задачам комбинаторики приводит подсчет вероятностей на основе гипотезы равновозможных элементарных событий.
Размещениями 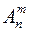 из
из  элементов по
элементов по 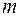 (
(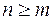 ) называют их соединения, каждое из которых содержит ровно
) называют их соединения, каждое из которых содержит ровно 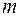 различных элементов (выбранных из данных элементов) и которые отличаются либо сами элементами, либо порядком элементов.
различных элементов (выбранных из данных элементов) и которые отличаются либо сами элементами, либо порядком элементов.
Определим число размещений 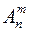 из
из  элементов
элементов 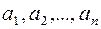 по
по 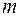 .
.
Будем строить произвольное соединение 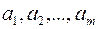 последовательно. Сначала определим его первый элемент
последовательно. Сначала определим его первый элемент 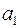 . Очевидно, что из данной совокупности
. Очевидно, что из данной совокупности  элементов его можно выбрать
элементов его можно выбрать  различными способами. После выбора первого элемента
различными способами. После выбора первого элемента 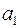 , для второго элемента
, для второго элемента 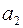 остается
остается 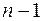 способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Для
способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Для 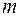 элементов формула приобретает вид:
элементов формула приобретает вид:
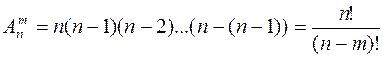
 2014-02-09
2014-02-09 934
934








