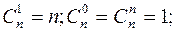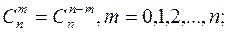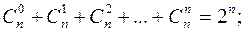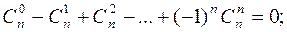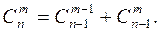Соединения из элементов, каждое из которых содержит все элементов, и которые отличаются лишь порядком элементов, называются перестановками

Перестановки являются частным случаем размещений. Так как каждая перестановка содержит все элементов множества, то различные перестановки отличаются друг от друга только порядком элементов.

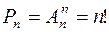
Сочетаниями 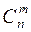из элементов по 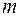(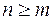) называют такие их соединения, каждое из которых содержит ровно 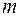данных элементов, и которые отличаются хотя бы одним элементом.

Рассмотрим все допустимые сочетания элементов .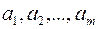

Делая в каждом из них 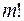возможных перестановок их элементов, очевидно, получим все размещения из элементов по :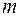

.

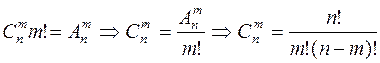Числа 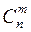являются коэффициентами в формуле бинома Ньютона:

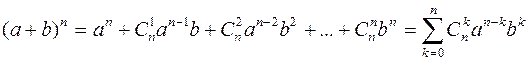
Свойства сочетаний:

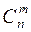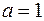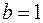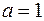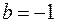Свойства 1 и 2 очевидно следуют из определения , свойства 3 и 4 доказываются с помощью бинома Ньютона, полагая для свойства 3 что и , а для свойства 4 что и . Свойство 5 можно проверить следующим образом:

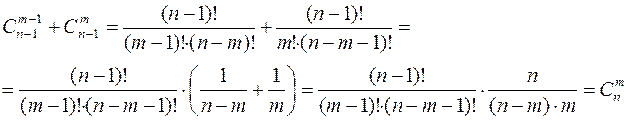
Это свойство позволяет последовательно вычислять биномиальные коэффициенты 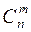с помощью так называемого треугольника Паскаля:

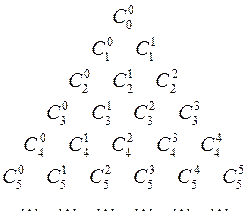
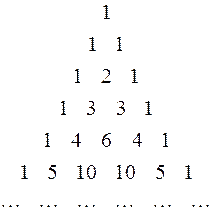
Здесь каждое число, кроме крайних единиц, является суммой двух вышерасположенных.