2014-02-09
517
И неравенства, и, наоборот, каждому решению уравнения
Соответствует единственное решение уравнения
Теорема. Каждому решению неравенства
.
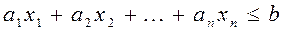
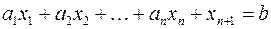
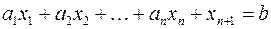
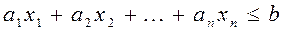Доказательство. Пусть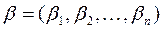 
– решение неравенства 
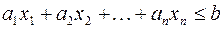. Тогда
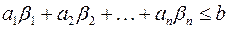или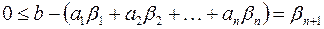 
Если в уравнение 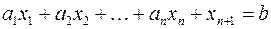вместо переменных подставить значения 
=
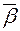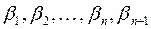, получится
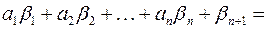
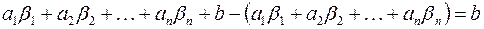
Таким образом, решение 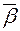удовлетворяет уравнению
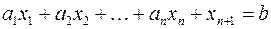
и неравенству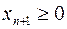 
. Доказана первая часть теоремы.
Пусть 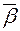удовлетворяет уравнению 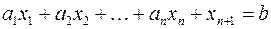и неравенству 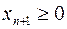, т.е. 
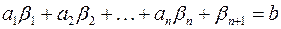и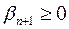 
. Отбрасывая в левой части равенства неотрицательную величину 
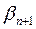, получим
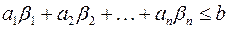
т.е. 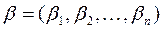удовлетворяет неравенству
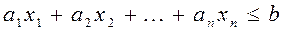
что и требовалось доказать.
Если в левую часть неравенств системы ограничений вида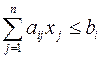 
, 
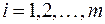добавить переменную 
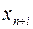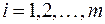, , то получится система ограничений – уравнений 
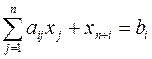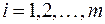, . В случае, если система неравенств–ограничений имеет вид 
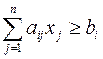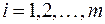, , то из левой части неравенств–ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную 
, .
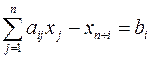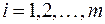Полученная таким образом система уравнений–ограничений, вместе с условиями неотрицательности переменных, т.е.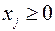 
, 
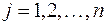и целевой функцией является канонической формой записи задачи линейного программирования.
Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах 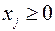, , 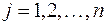а правые части - наличие производственных ресурсов, то числовые значения дополнительных неизвестных 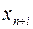, 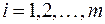означают объем неиспользованных ресурсов 
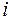-го вида.
Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.
