2014-02-09
975
Задача линейного программирования
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:
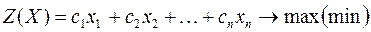
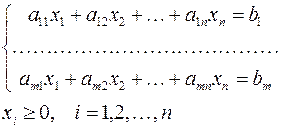
Используя знак суммирования эту задачу можно записать следующим образом:
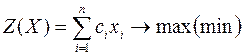
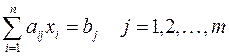
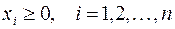
Каноническая задача линейного программирования в векторной форме имеет вид:
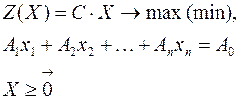
В данном случае введены векторы
, 
, 
, 
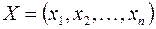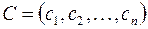
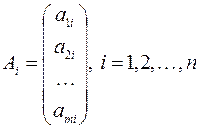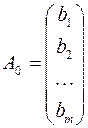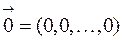
Здесь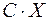 
– скалярное произведение векторов 
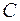и 
.
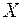Каноническая задача линейного программирования в матричной форме записи имеет вид
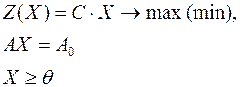
где
, .
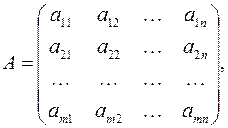
Здесь 
– матрица коэффициентов системы уравнений,
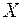– матрица-столбец переменных задачи; 
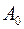– матрица-столбец правых частей системы ограничений.
Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:
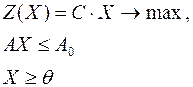или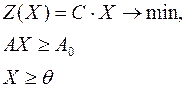 
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства
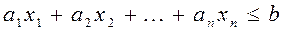
прибавляется величина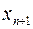 
, такая, что переводит неравенство в равенство 
,
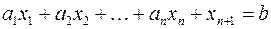где
.
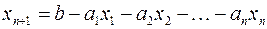Неотрицательная переменная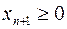 
называется дополнительнойпеременной.
Основания для возможности такого преобразования дает следующая теорема.
