Уравнение Клеро для геодезической линии

Линии

Система дифференциальных уравнений геодезической

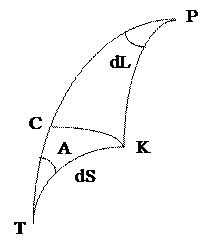
На рисунке 4. 5 имеем полярный сфероидический треугольник PTK,

Рис. 4. 5

у которого Р – полюс, T и K – бесконечно близкие друг другу точки, соединенные элементарной дугой геодезической линии dS, проходящей через точку T в азимуте А. Через точку К ( широта которой равна В) проведем параллель, которая пересечет меридиан точки Т в некоторой точке С. Рассмотрим элементарный прямоугольный треугольник ТСК у которого все стороны будут бесконечно малы потому, что гипотенуза dS по условию бесконечно мала. Этот треугольник решаем как плоский прямоугольный, при этом будем иметь в виду, что элементарная дуга меридиана ТС равна M dB, а параллели СК - rdL, где d L – разность долготточек К и Т. РЗ

В результате можем записать.

M dB = dS cos A; r dL = dS sin A, (4. 37)

откуда получаем дифференциальные зависимости

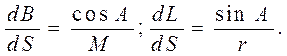(4. 38)

Обратимся теперь к треугольнику РTК. Не смотря на то, что одна из его сторон T К бесконечно мала, стороны РT и РК могут достигать значительных величин, зависящих от значения широты точки Т. В этом случае мы можем рассматривать его как сферический и решать по формулам сферической тригонометрии. Рассмотрим элементы этого треугольника. Угол при вершине Р равен dL, при вершине T – азимут А, сторона РТ выражается на сфере единичного радиуса как (p / 2 - В). Угол этого треугольника при вершине К можем определить как (p - А – d A), так как азимут геодезической линии в точке К равен (A + dA).

Применяя теорему косинуса угла для решения сферического треугольника РТК, имеем

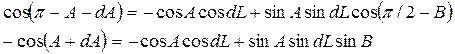
Применяя формулу для косинуса суммы и разлагая синусы и косинусы бесконечно малых аргументов в ряд и ограничиваясь первыми членами разложений, получим дифференциальное уравнение

,

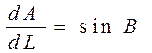в котором выражаем dL из второго уравнения (4. 38) в функции dA и запишем систему трех дифференциальных уравнений для геодезической линии эллипсоида в виде

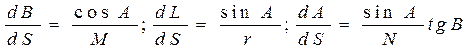(4. 39)

Система дифференциальных уравнений (4. 39) имеет очень большое значение. Оно лежит в основе решения задач сфероидической геодезии при определении связи между полярными координатами A и S и параметрическими координатами B и L на поверхности земного эллипсоида. Решение этих задач производится по формулам, следующим из интегрирования системы (4. 39).

Французский математик и геодезист Клеро в 1773 году взял первый интеграл системы вида (4. 39), описывающей геодезические линии на поверхностях вращения. Полученное уравнение в математике носит название уравнение Клеро для геодезических линий на поверхностях вращения.

Для вывода этого уравнения на поверхности земного эллипсоида перейдем в системе (4. 39) от геодезической широты В к приведенной широте u по ранее полученной формуле (3. 9) и формулам, следуемым из нее:

;

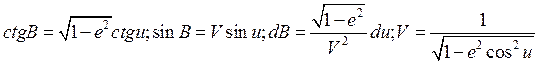с учетом этого система (4. 39) примет вид

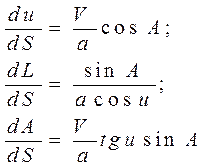(4. 40)

Разделив третье уравнение этой системы на первое, получим после очевидных преобразований

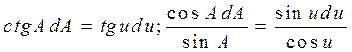
Интегрируя полученное уравнение, приходим к уравнению

,

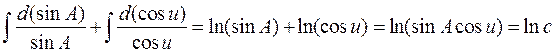откуда получаем уравнение Клеро для геодезической линии на поверхности земного эллипсоида

sinAcosu = c (4. 41)

Данное уравнение носит название теоремы Клеро, согласно которой произведение синуса азимута на косинус приведенной широты в каждой точке геодезической линии – величина постоянная.

Заметим геометрический смысл постоянной с в уравнении (4. 41). Полагая u = 0 (экваториальная точка), имеем c = sinA₀; при А=90⁰ (наиболее удаленная от экватора точка – точка вертекса) имеем c = cos u_В.

При использовании уравнения (4. 41) для вычислений широты по азимуту и наоборот заметим уравнение связи широт, следуемое из (3. 9)

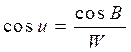
Если речь идет о двух фиксированных точках на поверхности эллипсоида, то справедливо будет уравнение связи

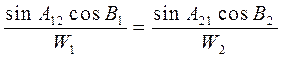
Вопросы для самоконтроля по разделу 4:

1. Какие плоскости образуют сопровождающий трехгранник кривой на поверхности?

2. Дать определения нормали к поверхности и главной нормали кривой.

3. Что такое кривизна кривой, ее составляющие?

4. Дать определения плоского сечения, нормального сечения и геодезической линии на поверхности.

5. Кривизна поверхности, главные радиусы кривизны поверхности земного эллипсоида.

6. Как определяется кривизна поверхности в произвольном азимуте?

7. Средний радиус поверхности в точке, для чего он используется в геодезии?

8. В чем особенности вычисления длины дуги меридиана земного эллипсоида?

9. Как вычисляют размеры рамок трапеций топографических карт? Какова точность вычислений?

10. Записать систему дифференциальных уравнений для геодезической линии эллипсоида.

11. Перейти в системе дифференциальных уравнений от геодезической к приведенной широте.

12. Записать уравнение Клеро для геодезической линии эллипсоида.