Т е м а. Уравнения в частных производных и методы их решения. Моделирование физических процессов. Эксперимент и математическая модель теплопроводности. Начальные и граничные условия.
Основной целью и предметом математической физики являются построение и исследование математических моделей физических явлений. Математическая физика, начиная со времен Ньютона, развивалась параллельно развитию физики и математики. Основные этапы ее становления и развития были связаны с решениями важнейших задач, имеющих теоретическое и практическое значение. В конце XVII века было открыто дифференциальное и интегральное исчисление (И. Ньютон, Г. Лейбниц) и были сформулированы основные законы классической механики и законы всемирного тяготения (И. Ньютон). Методы математической физики начали разрабатываться в XVIII веке при изучении колебания струны и стержня, а также при решении задач акустики и гидродинамики (Ж. Даламбер, Л. Эйлер, Д. Бернулли, Ж. Лагранж, П. Лаплас). В XIX веке идеи математической физики получили новое развитие в связи с задачами теплопроводности, диффузии, упругости, оптики, электродинамики, теории устойчивости и потенциала (Ж. Фурье, С. Пуассон, К. Гаусс, М.В. Остроградский, П. Дирихле, Б. Риман и др.). В XX веке предметом исследования математической физики становятся задачи квантовой физики, теории относительности, проблемы газовой динамики, переноса частиц и физики плазмы.
Многие задачи классической математической физики сводятся к краевым задачам для уравнений в частных производных. Приведем некоторые наиболее важные уравнения с частными производными.
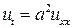 - -
| уравнение теплопроводности |
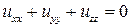 - -
| уравнение Лапласа |
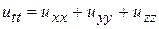 - -
| волновое уравнение |
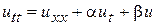 - -
| телеграфное уравнение |
Перечислим основные методы решения уравнений в частных производных.
1. Метод разделения переменных. Уравнение с частными производными с n независимыми переменными сводится к n обыкновенным дифференциальным уравнениям.
2. Метод интегральных преобразований. Уравнение с частными производными с n независимыми переменными сводится к уравнению с частными производными с (n - 1) независимыми переменными; следовательно, уравнение с частными производными с двумя независимыми переменными можно свести к обыкновенному дифференциальному уравнению.
3. Метод преобразования координат. Исходное уравнение с частными производными сводится к обыкновенному дифференциальному уравнению или к другому, более простому уравнению с частными производными с помощью соответствующего преобразования координат (например, поворота координатных осей и т.п.).
4. Преобразование зависимой переменной. Исходное уравнение с частными производными преобразуется к такому уравнению с частными производными для другой неизвестной функции, которое решается легче, чем исходное.
5. Численные методы. Исходное уравнение с частными производными сводится к системе разностных уравнений, которая решается методом итераций на ЭВМ.
6. Метод теории возмущений. Исходная нелинейная задача сводится к последовательности линейных задач, аппроксимирующих нелинейную задачу.
7. Метод функций Грина. Начальные и граничные условия заменяются системой простейших источников, и задача решается для каждого простейшего источника. Полное решение исходной задачи получается в результате суммирования решений для элементарных источников.
8. Метод интегральных уравнений. Уравнение с частными производными сводится к интегральному уравнению. Существует много различных методов решения интегральных уравнений.
9. Вариационные методы. Вместо уравнения с частными производными решается некоторая задача минимизации. Оказывается, что функция, доставляющая минимум некоторому выражению является в то же время решением исходного уравнения с частными производными.
10. Метод разложения по собственным функциям. Решение уравнения с частными производными ищется в виде ряда по собственным функциям. Эти собственные функции находятся как решения так называемой задачи на собственные значения, соответствующей исходной задаче для уравнения с частными производными.
Большинство физических явлений в таких областях как теплопередача, электричество, динамика жидкости могут быть описаны при помощи уравнений в частных производных. Начнем с рассмотрения физической задачи и дадим описание основных этапов простого эксперимента теплопроводности, на основе которого получим математическую модель теплопроводности, содержащую уравнения с частными производными. Эксперимент состоит в следующем:
1.Стержень длины 2 м и в диаметре 2 см с теплоизолированной боковой поверхностью поместим в устройство, поддерживающее внутри стержня некоторую постоянную температуру, например, 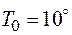 .
.
2.Извлечем стержень из этого устройства. Соответствующий момент времени будем считать равным нулю, то есть 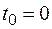 . Присоединим к концам стержня два термостата, поддерживающие на концах стержня постоянную температуру соответственно
. Присоединим к концам стержня два термостата, поддерживающие на концах стержня постоянную температуру соответственно 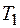 и
и 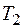 (например
(например 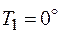 и
и 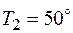 ).
).
3. Для наблюдения за изменением температуры на различных участках стержня, установим вдоль стержня термодатчики.
4. С течением времени температура на различных участках стержня будет меняться. При помощи датчиков зафиксируем данные о температуре. В результате получим температурные профили для различных моментов времени. Полученные данные о температуре и есть результаты эксперимента.
Рассмотрим теперь этапы построения математической модели. Заметим, что
1) по данным эксперимента температура на различных участках стержня разная для каждого фиксированного момента времени. Кроме того, на одном и том же участке в разное время температура разная. Следовательно, функция, характеризующая в рассматриваемом эксперименте изменение температуры, зависит от двух независимых переменных, от 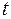 и
и 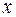 . Обозначим эту функцию через
. Обозначим эту функцию через 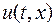 .
.
2) Согласно полученным экспериментальным путем профилям, скорость изменения температуры стержня в фиксированный момент времени 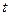 характеризуется степенью вогнутости профиля, то есть, пропорционален второй производной функции
характеризуется степенью вогнутости профиля, то есть, пропорционален второй производной функции 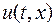 по переменной
по переменной 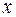 , определяющей выпуклость и вогнутость плоской кривой.
, определяющей выпуклость и вогнутость плоской кривой.
3) С другой стороны, скорость изменения температуры равна производной функции 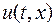 по времени
по времени 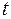 . Сравнивая эти две скорости, получим уравнение теплопроводности:
. Сравнивая эти две скорости, получим уравнение теплопроводности:
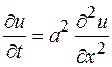 ,
, 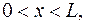
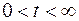 ,
,
где 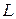 - длина стержня,
- длина стержня, 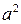 - коэффициент пропорциональности.
- коэффициент пропорциональности.
Все физические процессы начинаются в некоторый момент времени, условно принимаемый за 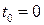 . В этот момент стержень обладает вполне определенной температурой
. В этот момент стержень обладает вполне определенной температурой 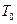 , то есть
, то есть 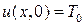 ,
, 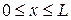 - начальное условие. По условиям задачи на концах стержня поддерживается постоянная температура, то есть
- начальное условие. По условиям задачи на концах стержня поддерживается постоянная температура, то есть 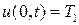 ,
, 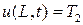 ,
, 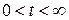 - граничные условия задачи. Если заданы только начальные условия, то соответствующая задача называется задачей Коши, если заданы граничные условия решения уравнения, то соответствующая задача называется краевой задачей. Если же заданы и начальные и граничные условия, то задача называется смешанной задачей.
- граничные условия задачи. Если заданы только начальные условия, то соответствующая задача называется задачей Коши, если заданы граничные условия решения уравнения, то соответствующая задача называется краевой задачей. Если же заданы и начальные и граничные условия, то задача называется смешанной задачей.
Т е м а. Математическая модель колебания струны. Ограничения и оценка погрешности моделирования. Начальные и граничные условия. Общая классификация уравнений в частных производных. Линейные и квазилинейные уравнения в частных производных первого порядка и их решение.
Рассмотрим малые колебания струны с закрепленными концами. Предположим, что струна туго натянута, сделана из однородного материала и колеблется в одной плоскости. Действием сил тяжести на струну будем пренебрегать.
Пусть в положении равновесия струна расположена вдоль оси Ox. Будем рассматривать только поперечные колебания струны, считая, что перемещение частиц струны происходит в одной плоскости и все точки струны движутся перпендикулярно оси Ox.
Обозначим через 
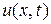 отклонение от положения равновесия точки струны с абсциссой x в момент времени t.
отклонение от положения равновесия точки струны с абсциссой x в момент времени t.
Для построения математической модели колебаний струны рассмотрим все силы, действующие на небольшой участок струны (рис. 1).
u


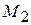
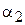




 T
T

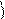

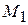
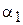
T

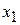
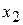 x
x
Рис. 1. Малый участок, колеблющейся струны.
Силы натяжения, возникающие в струне, всегда направлены по касательным к ее мгновенному профилю. Это условие выражает собой то, что струна не сопротивляется изгибу.
Выделим элемент струны 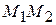 , который при равновесии занимал положение
, который при равновесии занимал положение 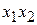 . Рассмотрим только малые поперечные колебания струны, когда смещения u и производные
. Рассмотрим только малые поперечные колебания струны, когда смещения u и производные 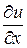 столь малы, что их квадратами и произведениями можно пренебречь по сравнению с значениями самих величин. Пусть a - острый угол, образованный направлением касательной к струне с осью Ox. Мы имеем:
столь малы, что их квадратами и произведениями можно пренебречь по сравнению с значениями самих величин. Пусть a - острый угол, образованный направлением касательной к струне с осью Ox. Мы имеем:
tg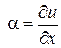 и
и 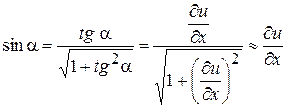 .
.
Из предположения о малости колебаний следует, что длина выделенного участка струны в любой момент времени равна:
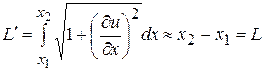 .
.
Это означает, что в процессе малых колебаний удлинением участков струны можно пренебречь. В этом случае, согласно закону Гука, натяжение T не меняется со временем, и не зависит от x, т.е. одинакова во всех точках струны.
Рассмотрим элемент струны 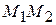 . На концах этого элемента, по касательным к струне, действуют силы натяжения T. Пусть касательные образуют с осью Ox углы a и a+Da. Тогда проекция на ось Ou сил, действующих на элемент
. На концах этого элемента, по касательным к струне, действуют силы натяжения T. Пусть касательные образуют с осью Ox углы a и a+Da. Тогда проекция на ось Ou сил, действующих на элемент 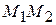 , будет равна
, будет равна 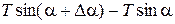 . Так как угол a мал, то мы будем иметь:
. Так как угол a мал, то мы будем иметь:
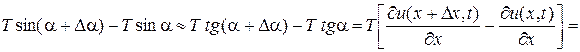
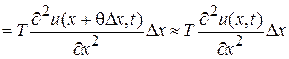 ,
, 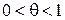 .
.
(здесь мы применили теорему Лагранжа к выражению, стоящему в квадратных скобках).
Внешняя сила 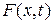 , приложенная к струне, может произвольным образом зависеть от x и от t.
, приложенная к струне, может произвольным образом зависеть от x и от t.
Чтобы получить уравнения движения, нужно внешние силы, приложенные к элементу, приравнять силе инерции (второй закон Ньютона) – которая равна произведению массы этого элемента на его ускорение. Пусть r - линейная плотность струны. Тогда масса элемента струны будет 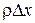 . Ускорение элемента равно
. Ускорение элемента равно 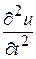 . Следовательно, будем иметь:
. Следовательно, будем иметь:
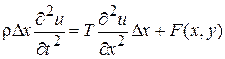 . (1)
. (1)
Сокращая на D x и обозначая 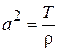 и
и 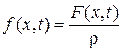 , получаем уравнение движения
, получаем уравнение движения
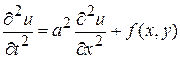 . (2)
. (2)
Это и есть волновое уравнение – уравнение колебания струны.
Если 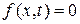 , то однородное уравнение
, то однородное уравнение
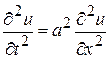 (3)
(3)
описывает свободные колебания струны без воздействия вынуждающей силы.
Общая классификация уравнений в частных производных
Общий вид уравнений с частными производными порядка можно записать в виде соотношений между независимыми переменными, искомой функцией u и ее частными производными первого, второго порядков и выше:
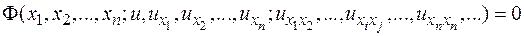 .
.
Порядком уравнения в частных производных называется наивысший порядок частных производных, входящих в это уравнение. Уравнение в частных производных называется линейным, если является линейной комбинацией частных производных и некоторых функций от независимых переменных, являющихся коэффициентами этого уравнения. Если эти функции зависят также от искомой функции u, то уравнение называется квазилинейным. Уравнения, не являющиеся линейными или квазилинейными, называются нелинейными уравнениями в частных производных. Если уравнение содержит в качестве слагаемого функцию, зависящую только от независимых переменных, то уравнение в частных производных называется неоднородным, в противном случае – однородным.
Рассмотрим линейное уравнение первого порядка от двух независимых переменных
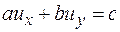 , (4)
, (4)
где a, b, c – некоторые функции от независимых переменных и искомой функции, имеющие в рассматриваемой области непрерывные частные производные первого порядка и удовлетворяющие условию 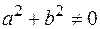 . Решение этого уравнения представляет собой некоторую поверхность, называемую интегральной поверхностью.
. Решение этого уравнения представляет собой некоторую поверхность, называемую интегральной поверхностью.
Пусть 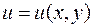 - решение уравнения (4). На этой интегральной поверхности зададим однопараметрическое семейство кривых
- решение уравнения (4). На этой интегральной поверхности зададим однопараметрическое семейство кривых
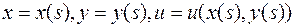 .
.
Дифференцируя функцию 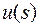 по
по 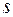 , получим
, получим
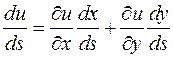 . (5)
. (5)
Сравнивая с уравнением (4) заметим, что семейство кривых, покрывающих интегральную поверхность, можно определить как решения дифференциальных уравнений
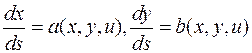 .
.
При этом исходное уравнение (4) преобразуется в следующее уравнение
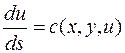 .
.
 2014-02-09
2014-02-09 560
560








