Уравнения

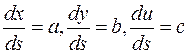
или

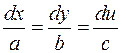
называются характеристическими уравнениями.

Задача Коши. Пусть 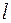- пространственная кривая, заданная в параметрической форме 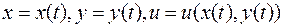, а 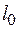- проекция кривой 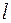на плоскость 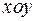. Найти решение уравнения (4), принимающее заданные значения в точках кривой .

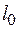Условия существования решение задачи Коши являются содержанием следующей теоремы.

Теорема. Если 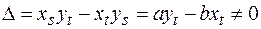всюду на кривой 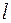, то задача Коши для уравнения (4) имеет одно и только одно решение. Если 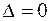на 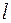, то для того, чтобы задача Коши имела решение необходимо, чтобы кривая 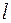была характеристикой уравнений (4). В этом случае задача Коши имеет бесконечно много решений.