Пусть:
область, которая разрешена ограничениями
 |


 g1(x)=0 Ñf g2(x)=0
g1(x)=0 Ñf g2(x)=0
 точка минимума
точка минимума



 f = const (линия уровня)
f = const (линия уровня)

 Ñg1 Ñg2
Ñg1 Ñg2
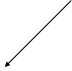
-Ñf
 |  |
конус
Тогда -Ñf представляется так:
-Ñf = l1Ñg1+l2Ñg2, где l1³0, l2³0.(1)
-Ñf расположен в конусе, образованном Ñg1 и Ñg2.
(1) переписывается так:
Ñf + 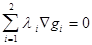 , где li - множители Лагранжа.
, где li - множители Лагранжа.
По рисунку li gi (x) = 0 (мы попадаем на границу). Тогда можно рассматривать функцию Лагранжа f + 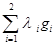 и считать стационарную точку так, будто нет ограничений. Переход от равенств к неравенствам накладывает ограничения на li
и считать стационарную точку так, будто нет ограничений. Переход от равенств к неравенствам накладывает ограничения на li
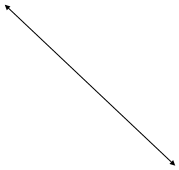
(li ³0). Пусть Ñf направлен иначе (-Ñf находится не в конусе), тогда иллюстрация.
Иллюстрация:
 |
 S g2(x) = 0
S g2(x) = 0
 g1(x) = 0
g1(x) = 0

 -Ñf
-Ñf

 Ñg1 конус Ñg2
Ñg1 конус Ñg2
В этом случае есть выбор S, которое составляет острый угол с -Ñf и тупой с Ñg1 иÑg2.
То есть, если пойдем по S, то наши ограничения будут выполняться (в тоже время функция будет убывать), и эта точка не будет extr.
Таким образом, чтобы точка была экстремальной, антиградиент должен лежать в соответствующем конусе.
Рассмотрим другую точку на g2(x) = 0.

 Ñf1 g2(x) = 0
Ñf1 g2(x) = 0
 |
Ñg2
Если Ñf1 направлен так, как показано, то точка будет подозрением на extr. Необходимое условие записывается также, но в этом случае l1=0 (то есть не рассматривается g1).
Пусть x*- экстремальная точка, свяжем с x* множество индексов активных ограничений: 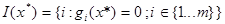
Лемма:
Ïóñòü 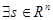 - некоторый вектор, удовлетворяющий следующим свойствам:
- некоторый вектор, удовлетворяющий следующим свойствам:
(*)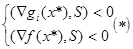 ,тогда точка x* - не экстремальная.
,тогда точка x* - не экстремальная.
Доказательство:
Идея:
Показать, что на луче с вершиной x* и направлением S будут лежать вблизи вершины некоторые точки, которые будут допустимыми и в них целевая функция строго меньше чем в точке x*
Пусть e>0
(1)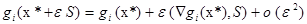
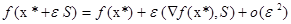 (разложение в полином Тейлора)
(разложение в полином Тейлора)
тогда (см. определение I(x*)).
Тогда (см.(1)).
Если 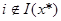 , то
, то 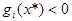 . Отсюда
. Отсюда 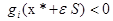 (e- достаточно мало).
(e- достаточно мало).
Таким образом, при достаточно малых e, точка x* + eS- допустима, кроме этого функция f на этом луче убывает. Таким образом точка x* не является экстремальной. Для экстремальной точки x* система неравенств (*) - несовместна.
Лемма Фаркаша:
Пусть есть матрица А(m ´ n), тогда справедливо одно из следующих двух условий:
1) 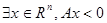
2) 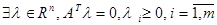
 2014-02-09
2014-02-09 652
652








