Задача выпуклого программирования
min f =? X- допустимое множество
X=íxÎRn, gi(x)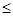 0, i =1...mý f и все gi выпуклы
0, i =1...mý f и все gi выпуклы
Утверждение:
Допустимое множество в задаче выпуклого программирования (ЗВП) выпукло
Доказательство:
пусть x1,x2ÎX, lÎ[0,1]
lx1+(1-l)x2ÎX
воспользуемся свойством выпуклости gi:
gi(lx1+(1-l)x2)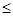
 l gi (x1) + (1-
l gi (x1) + (1- ) gi(x2)
) gi(x2)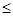 0
0
тогда  x1+(1-
x1+(1- )x2
)x2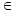 X (см. опр. X),но рассматривается только отдельная gi.
X (см. опр. X),но рассматривается только отдельная gi.
Все допустимое множество X рассматривается как пересечение выпуклых
множеств 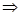 X выпукло.
X выпукло.
Определение:
Функцией Лагранжа в ЗВП называется функция
f(x)+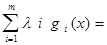 f(x) + (
f(x) + ( ,g(x)), где
,g(x)), где  i
i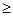 0
0
справедлива теорема Каруша-Джона:
Ñf(x*)+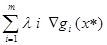 =0,
=0,  i gi(x*) = 0, i=1..m
i gi(x*) = 0, i=1..m
В случае выпуклости множества X условие линейной независимости векторов
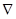 gi(x), соответствующее активным ограничениям, можно заменить более просто
gi(x), соответствующее активным ограничениям, можно заменить более просто
проверяемыми, а именно, так называемыми условиями регулярности.
Существуют различные условия регулярности ограничений:
А) если для любого i (1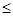 i
i 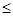 m)
m)
существует xi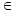 X: gi (xi) <0, то говорят, что множество X удовлетворяет
X: gi (xi) <0, то говорят, что множество X удовлетворяет
условию регулярности.
Б) условие регулярности Слейтера:
Существует точка x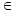 X такая, что для любого i=1...m gi(x)<0.
X такая, что для любого i=1...m gi(x)<0.
Легко доказать эквивалентность условий А и Б. Очевидно, что из Б
следует А. Пусть теперь выпукла А. Выберем x =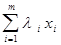 ,
, 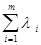 =1,
=1,
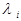
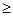 0, i=1...m
0, i=1...m это возможно, так как X выпукло.
это возможно, так как X выпукло.
Тогда Б следует из неравенства Иенсена.
Замечание:
Условие регулярности означает, что допустимое множество имеет внутреннюю
точку (то есть оно не вырождено в точку(общий случай))
Определение:
Пусть существует функция 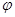 (x,y), точка (x
(x,y), точка (x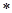 ,y
,y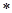 ) называется седловой точкой функции
) называется седловой точкой функции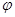 , если выполняется следующее неравенство: (x,y)
, если выполняется следующее неравенство: (x,y)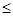
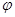 (x
(x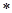 ,y
,y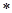 )
)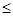
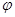 (x,y
(x,y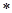 )
)
Теорема (о седловой точке):
Пусть функция Лагранжа ЗВП имеет седловую точку, то есть
f(x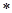 )+
)+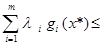 f(x
f(x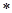 )+
)+ 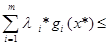 f (x)+
f (x)+ 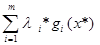
для любого xÎRn, li ³0, i =1...m
тогда x*- оптимальная точка (решение) ЗВП.
Доказательство:
Из левого неравенства следует:
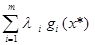
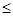
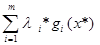 ,li* ³0, gi(x*)
,li* ³0, gi(x*)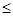 0(см. опред. X)
0(см. опред. X)
Так как  -любое, то при
-любое, то при  =0 получится:
=0 получится:
0£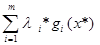
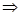 (l*, g(x*))=0.
(l*, g(x*))=0.
Из правого неравенства имеем:
f(x*)+0 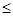 f(x)+
f(x)+ 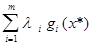
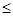 f(x)
f(x) 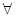 x
x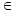 X
X
Тогда по определению оптимальной точки x*оптимальна.
Теорема Куна-Таккера:
Пусть в ЗВП выполнено условие регулярности Слейгера. Тогда для того, чтобы
x* была оптимальной точкой ЗВП, необходимо и достаточно, чтобы для
некоторого вектора l* с неотрицательными компонентами точка (x*,l*)
была седловой точкой функции Лагранжа.
Доказательство:
Достаточность следует из теоремы о седловой точке.
Необходимость -без доказательства.
 2014-02-09
2014-02-09 883
883








