Задача нелинейного программирования.
Условная минимизация.
min f -?, на множестве X.
Нелинейная область: 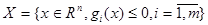 - допустимое множество.
- допустимое множество.
ji- некоторые функции.
рассмотрим 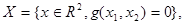 найти
найти 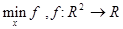 .
.
Ïóñòü g разрешима относительно x1, то есть x1= g(x2).
Тогда 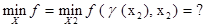
Пусть f, g - дифференцируемы. Тогда условие экстремальности: 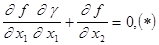 , так как
, так как 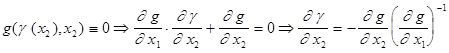
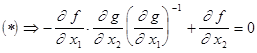
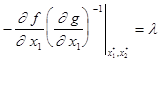
Тогда:
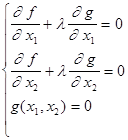 , из определения l
, из определения l
Таким образом в точке минимума выполняются эти соотношения. Получить эти необходимые условия можно используя функцию Лагранжа:
F(x,l)=f+lg.
Тогда необходимое условие min функции f(x1,x2) при наличии ограничений может быть записано следующим образом:
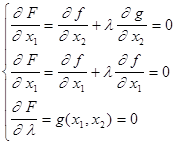
 2014-02-09
2014-02-09 479
479








