Классы Поста. Теорема Поста.
1) Функции, сохраняющие const «0» – Р 0.
Свойство: 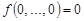 , на нулевом наборе имеет значение «нуль».
, на нулевом наборе имеет значение «нуль».
Пример: 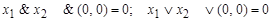 .
.
(& и Ú) Î P 0; x 1ç x2; функция Шеффера ç(0, 0)=;|Ï P 0.
2) Функции, сохраняющие const «1» – Р 1
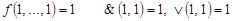 .
.
(& и Ú) Î P 1; |(1, 1) = 0;| Ï P 1.
3) Самодвойственные функции – S
Введём оператор двойственности D, он преобразует ФАЛ в соответствии с определением.
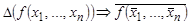
Пример:
| x 1, x 2 | & | Þ | x 1×× x 2 | D | º | x 1, x 2 | D |
| 0 0 0 1 1 0 1 1 | 1 1 1 0 0 1 0 0 | 0 0 0 1 1 0 1 1 |
табл. 1. & табл. 2. 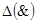 табл. 3.
табл. 3. 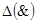
ФАЛ называется самодвойственной, если
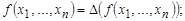 ù Î S.
ù Î S.
Пример 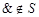 ; сравни табл. 1.& с табл. 3. D(&)
; сравни табл. 1.& с табл. 3. D(&)
Пример: ù (отрицание); ùÎ S
| х | ù | х | Dù | |
| = |
4) Линейные функции – L
ФАЛ называется линейной, если она представима в виде: 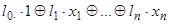 , где
, где 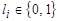
Примеры: а) 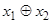 представима в виде
представима в виде
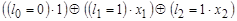
б) 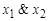 не представима; доказывается перебором значений вектора l, & Ï L
не представима; доказывается перебором значений вектора l, & Ï L
5) Монотонные функции – М
Введём отношение предшествования двух наборов
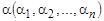 и
и 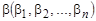
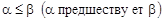 если все элементы в наборах находятся в отношении
если все элементы в наборах находятся в отношении 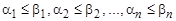 .
.
Пример: а) 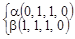
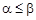 ;
;
б) 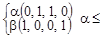
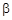 и
и 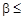
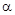 . Наборы не сравнимы.
. Наборы не сравнимы.
ФАЛ называется монотонной, если 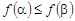 для всех a i и b i таких, что
для всех a i и b i таких, что 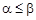 .
.
Сравнение наборов и значений функций удобно проверить на гиперкубе.
Примеры.
а) Грань для ФАЛ с двумя переменными, на которой отмечена функция дизъюнкции.
Наборы: (11) >(01); (11) > (00); (11) > (10); (10) > (00); (01) > (00).
Функция: 1 = 1; 1 > 0; 1 = 1; 1 > 0; 1 > 0;
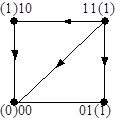
Дизъюнкция «Ú» относится к классу монотонных функций 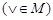 .
.
б) Конъюнкция &
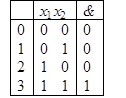
(11) > (01); (11) > (00); (11) > (10); (10) > (00); (01) > (00).
1 > 0; 1 > 0; 1 > 0; 0 = 0; 0 = 0.
Конъюнкция «&» относится к классу монотонных функций 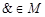 .
.
в) Сложение по mod2 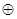 не является монотонной
не является монотонной
| x 1 x 2 | Å | |
| 0 0 0 1 1 0 1 1 |
(11) > (01); (11) > (00); (11) > (10); (10) > (00); (01) > (00).
1 < 0; 0 = 0; 0 < 1; 1> 0; 1 > 0.
Теорема Поста. Набор 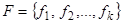 , будет полным, если он содержит функции не принадлежащие к P 0, P1, S, L, M.
, будет полным, если он содержит функции не принадлежащие к P 0, P1, S, L, M.
Классы P 0, P1, S, L, M называются предполными классами Поста. Если задана система функций, то её можно тестировать на полноту, составляя для нее, т.н. таблицу Поста.
Таблица Поста для восьми элементарных функций («+» отмечена принадлежность к классу).
| Функция | Р 0 | Р 1 | S | L | M | |
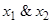
| + | + | – | – | + | |
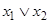
| + | + | – | – | + | |
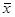
| – | – | + | + | – | |
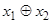
| + | – | – | + | – | |
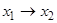
| – | + | – | – | – | |
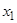 ï ï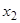
| – | – | – | – | – | |
| – | + | – | + | + | ||
| + | – | – | + | + |
По этой таблице можно выбрать min наборы, которые еще называются базовыми наборами.
1) {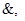 ù};
ù}; 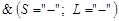 ; ù
; ù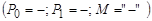 . Этот набор является базовым.
. Этот набор является базовым.
Базовым набором будет единственная функция | – штрих Шеффера. Если задана система функций, то можно проверить ее на полноту.
2) Таблица Поста для 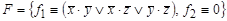 .
.
| Р 0 | Р 1 | S | L | M | |
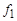
| – | – | + | – | – |
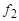
| + | – | – | + | + |
Система F = { f 1, f 2} является полной.
3) Таблица Поста для 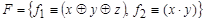 .
.
| Р 0 | Р 1 | S | L | M | |
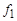
| + | + | + | + | + |
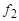
| + | + | – | – | + |
Система F = { f 1, f 2} является неполной.
Свойства полных наборов
| №№ п/п | Полные наборы | Свойства |
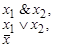
| Булева Алгебра | |
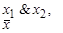
| Переход к дизъюнкции 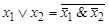
| |
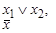
| Переход к конъюнкции 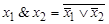
| |
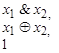
| 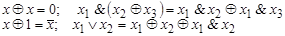
| |
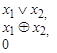
| 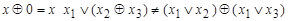
| |
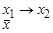
| 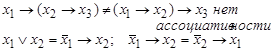
| |
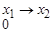
| 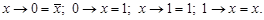
| |
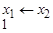
| 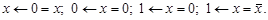
|
Содержание:
7.1. Классификация САПР УП........................................................................................................................................... 1
7.2. Структура и состав САПР УП................................................................................................................................... 2
7.3. Показатели уровня САПР УП.................................................................................................................................... 6
7.4. Характеристики современных САПР УП............................................................................................................... 6
 2014-02-09
2014-02-09 407
407







