Экскурс в математику

I) Если функция f(х) имеет разложение по различным ортогональным системам функций φ_n(х), т. е. f(х) есть кусочно-заданная функция и если:

1) предполагается, что на отрезке [a;b]

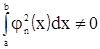, (8.3)

а величина

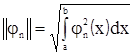(8.4)

называется нормой функции φ_n(х),

2) то функция φ_n(х), для которой выполняется условие:

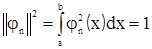, (8.5)

называется нормированной функцией,

3) система нормированных функций φ₁(х), φ₂(х),..., в которой каждые две различные функции взаимно ортогональны, называются ортонормированной системой функций.

II) В математике также доказывается, что если φ_n(х) – непрерывна, то произвольная кусочно-непрерывная функция f(х), для которой выполняется условие

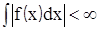, (8.6)

может быть представлена в виде суммы ряда (8.7):

(8.7)

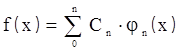
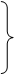
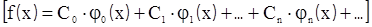
(8.7) называется обобщенным рядом Фурье. А совокупность коэффициентов

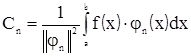, (8.8)

называется спектром сигнала f(х) в ортогональной системе функций φ_n(х).

Применительно к нашему сигналу S(t) (8.7) можно переписать:

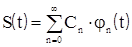, (8.9)

а квадрат нормы функции S(t)

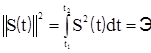, (8.10)

где Э – энергия импульса [сравним c (8.1)]. При этом средняя мощность сигнала

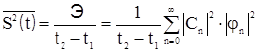. (8.11)

8.3. Гармонический анализ периодических сигналов

При разложении сигнала S(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут:

1. Систему тригонометрических функций

cosω₁t, sin ω₁t, cosω₂t, sin ω₂t,... (8.12)

либо

2. Систему ортогональных функций в комплексной форме:

..., е^-i2ω₁^t, е^-iω₁^t, е^iω₁^t, е^i2ω₁^t,... (8.13)

Интервал ортогональности в обоих случаях совпадает с периодом 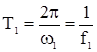функции S(t).

Система функций (8.12) приводит к тригонометрической форме ряда Фурье, а система (8.13) – к комплексной форме.

Опуская промежуточные преобразования, для периодического сигнала S(t) запишем:

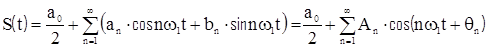, где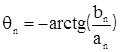. (8.14)

Здесь, амплитуда n-й гармоники A_n: 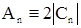, a ;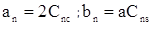

(a_n – коэффициент при cos, а b_n – при sin).

Амплитуды гармонических составляющих могут быть определены с помощью формул Эйлера для коэффициентов ряда Фурье.

Таким образом, для всех положительных n (включая n=0):

(8.15)

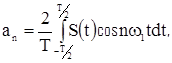
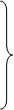
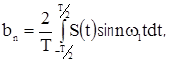
Здесь 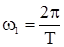– основная частота последовательности, образующей периодический сигнал от 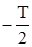до .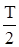

Спектры периодических функций называют линейчатыми или дискретными. Так как они состоят из отдельных линий, соответствующих отдельным частотам 0, ω₁, ω₂ =2ω₁, ω₃ =3ω₁ и т. д.

Совокупность А_n называют спектром амплитуд.